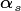1. Technical Documentation for FATES¶
FATES is the “Functionally Assembled Terrestrial Ecosystem Simulator”. It is an external module which can run within a given “Host Land Model” (HLM). Currently (November 2017) implementations are supported in both the Community Land Model of the Community Terrestrial Systems Model (CLM-CTSM) and in the Energy Exascale Earth Systems Model (E3SM) Land Model (ELM).
FATES was derived from the CLM Ecosystem Demography model (CLM(ED)), which was documented in:
Fisher, R. A., Muszala, S., Verteinstein, M., Lawrence, P., Xu, C., McDowell, N. G., Knox, R. G., Koven, C., Holm, J., Rogers, B. M., Spessa, A., Lawrence, D., and Bonan, G.: Taking off the training wheels: the properties of a dynamic vegetation model without climate envelopes, CLM4.5(ED), Geosci. Model Dev., 8, 3593-3619, https://doi.org/10.5194/gmd-8-3593-2015, 2015.
and this technical note was first published as an appendix to that paper.
https://pdfs.semanticscholar.org/396c/b9f172cb681421ed78325a2237bfb428eece.pdf
1.2. Introduction¶
The Ecosystem Demography (‘ED’), concept within FATES is derived from the work of Moorcroft et al. (2001)
and is a cohort model of vegetation competition and co-existence, allowing a representation of the biosphere which accounts for the division of the land surface into successional stages, and for competition for light between height structured cohorts of representative trees of various plant functional types.
The implementation of the Ecosystem Demography concept within FATES links the surface flux and canopy physiology concepts in the CLM/ELM with numerous additional developments necessary to accommodate the new model also documented here. These include a version of the SPITFIRE (Spread and InTensity of Fire) model of Thonicke et al. (2010), and an adoption of the concept of Perfect Plasticity Approximation approach of Purves et al. 2008, Lichstein et al. 2011 and Weng et al. 2014, in accounting for the spatial arrangement of crowns. Novel algorithms accounting for the fragmentation of coarse woody debris into chemical litter streams, for the physiological optimisation of canopy thickness, for the accumulation of seeds in the seed bank, for multi-layer multi-PFT radiation transfer, for drought-deciduous and cold-deciduous phenology, for carbon storage allocation, and for tree mortality under carbon stress, are also included and presented here.
Numerous other implementations of the Ecosystem Demography concept exist (See Fisher et al. (2018) for a review of these) Therefore, to avoid confusion between the concept of ‘Ecosystem Demography’ and the implementation of this concept in different models, the CLM(ED) implementation described by Fisher et al. (2015) will hereafter be called ‘FATES’ (the Functionally Assembled Terrestrial Ecosystem Simulator).
1.3. The representation of ecosystem heterogeneity in FATES¶
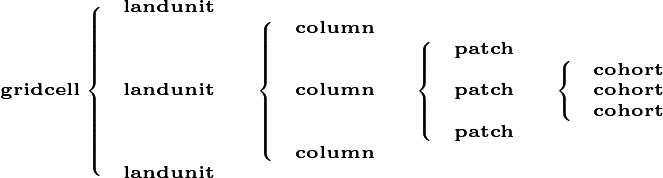
The terrestrial surface of the Earth is heterogeneous for many reasons, driven by variations in climate, edaphic history, ecological variability, geological forcing and human interventions. Land surface models represent this variability first by introducing a grid structure to the land surface, allowing different atmospheric forcings to operate in each grid cell, and subsequently by representing ‘sub-grid’ variability in the surface properties. In the CLM, the land surface is divided into numerous ‘landunits’ corresponding to the underlying condition of the surface (e.g. soils, ice, lakes, bare ground) and then ‘columns’ referring to elements of the surface that share below ground resources (water & nutrients). Within the soil landunit, for example, there are separate columns for crops, and for natural vegetation, as these are assumed to use separate resource pools. The FATES model at present only operates on the naturally vegetated column. The soil column is sub-divided into numerous tiles, that correspond to statistical fractions of the potentially vegetated land area. In the CLM 4.5 (and all previous versions of the model), sub-grid tiling operates on the basis of plant functional types (PFTs). That is, each piece of land is assumed to be occupied by only one plant functional type, with multiple PFT-specific tiles sharing a common soil water and nutrient pool. This PFT-based tiling structure is the standard method used by most land surface models deployed in climate prediction.
The introduction of the Ecosystem Demography concept introduces significant alterations to the representation of the land surface in the CLM. In FATES, the tiling structure represents the disturbance history of the ecosystem. Thus, some fraction of the land surface is characterized as ‘recently disturbed’, some fraction has escaped disturbance for a long time, and other areas will have intermediate disturbances. Thus the ED concept essentially discretizes the trajectory of succession from disturbed ground to ‘mature’ ecosystems. Within FATES, each “disturbance history class” is referred to as a ‘patch’. The word “patch” has many possible interpretations, so it is important to note that: there is no spatial location associated with the concept of a ‘patch’ . It refers to a fraction of the potential vegetated area consisting of all parts of the ecosystem with similar disturbance history.
The ‘patch’ organizational structure in CLM thus replaces the previous ‘PFT’ structure in the organization heirarchy. The original hierarchical land surface organizational structure of CLM as described in Oleson et al. 2013 may be depicted as:

and the new structure is altered to the following:

Thus, each gridcell becomes a matrix of ‘patches’ that are conceptualized by their ‘age since disturbance’ in years. This is the equivalent of grouping together all those areas of a gridcell that are ‘canopy gaps’, into a single entity, and all those areas that are ‘mature forest’ into a single entity.
1.3.1. Cohortized representation of tree populations¶
Each common-disturbance-history patch is a notional ecosystem that might in reality contain numerous individual plants which vary in their physiological attributes, in height and in spatial position. One way of addressing this heterogeneity is to simulate a forest of specific individuals, and to monitor their behavior through time. This is the approach taken by “gap” and individual-based models (Smith et al. 2001, Sato et al. 2007, Uriarte et al. 2009, Fyllas et al. 2014). The depiction of individuals typically implies that the outcome of the model is stochastic. This is because we lack the necessary detailed knowledge to simulate the individual plant’s fates. Thus gap models imply both stochastic locations and mortality of plants. Thus, (with a genuinely random seed) each model outcome is different, and an ensemble of model runs is required to generate an average representative solution. Because the random death of large individual trees can cause significant deviations from the mean trajectory for a small plot (a typical simulated plot size is 30m x 30 m) the number of runs required to minimize these deviations is large and computationally expensive. For this reason, models that resolve individual trees typically use a physiological timestep of one day or longer (e.g. Smith et al. 2001, Xiaidong et al. 2005, Sato et al. 2007
The approach introduced by the Ecosystem Demography model
Moorcroft et al. 2001 is to group the hypothetical population
of plants into “cohorts”. In the notional ecosystem, after the
land-surface is divided into common-disturbance-history patches, the
population in each patch is divided first into plant functional types
(the standard approach to representing plant diversity in large scale
vegetation models), and then each plant type is represented as numerous
height classes. Importantly, for each PFT/height class bin, we model
*one* representative individual plant, which tracks the average
properties of this `cohort` of individual plants. Thus, each
common-disturbance-history patch is typically occupied by a set of
cohorts of different plant functional types, and different height
classes within those plant functional types. Each cohort is associated
with a number of identical trees,  (where
(where 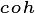 denotes the identification or index number for a given cohort)..
denotes the identification or index number for a given cohort)..
The complete hierarchy of elements in FATES is therefore now described as follows:
1.3.2. Discretization of cohorts and patches¶
Newly disturbed land and newly recruited seedlings can in theory be generated at each new model timestep as the result of germination and disturbance processes. If the new patches and cohorts established at every timestep were tracked by the model structure, the computational load would of course be extremely high (and thus equivalent to an individual-based approach). A signature feature of the ED model is the system by which functionally equivalent patches and cohorts are fused into single model entities to save memory and computational time.
This functionality requires that criteria are established for the
meaning of functional equivalence, which are by necessity slightly
subjective, as they represent ways of abstracting reality into a more
tractable mathematical representation. As an example of this, for
height-structured cohorts, we calculate the relativized differences in
height ( , m) between two cohorts of the same pft,
, m) between two cohorts of the same pft,
 and
and  as
as
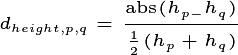
If  is smaller than some threshold
is smaller than some threshold 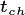 ,
and they are of the same plant functional type, the two cohorts are
considered equivalent and merged to form a third cohort
,
and they are of the same plant functional type, the two cohorts are
considered equivalent and merged to form a third cohort 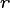 , with
the properties of cohort
, with
the properties of cohort  and
and  averaged such that they
conserve mass. The model parameter
averaged such that they
conserve mass. The model parameter 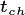 can be adjusted to
adjust the trade-off between simulation accuracy and computational load.
There is no theoretical optimal value for this threshold but it may be
altered to have finer or coarser model resolutions as needed.
can be adjusted to
adjust the trade-off between simulation accuracy and computational load.
There is no theoretical optimal value for this threshold but it may be
altered to have finer or coarser model resolutions as needed.
Similarly, for common-disturbance-history patches, we again assign
a threshold criteria, which is then compared to the difference between
patches  and
and  , and if the difference is less than some
threshold value (
, and if the difference is less than some
threshold value (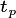 ) then patches are merged together,
otherwise they are kept separate. However, in contrast with
height-structured cohorts, where the meaning of the difference criteria
is relatively clear, how the landscape should be divided into
common-disturbance-history units is less clear. Several alternative
criteria are possible, including Leaf Area Index, total biomass and
total stem basal area.
) then patches are merged together,
otherwise they are kept separate. However, in contrast with
height-structured cohorts, where the meaning of the difference criteria
is relatively clear, how the landscape should be divided into
common-disturbance-history units is less clear. Several alternative
criteria are possible, including Leaf Area Index, total biomass and
total stem basal area.
In this implementation of FATES we assess the amount of
above-ground biomass in each PFT/plant diameter bin. Biomass is first
grouped into fixed diameter bins for each PFT (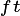 ) and a
significant difference in any bin will cause patches to remain
separated. This means that if two patches have similar total biomass,
but differ in the distribution of that biomass between diameter classes
or plant types, they remain as separate entities. Thus
) and a
significant difference in any bin will cause patches to remain
separated. This means that if two patches have similar total biomass,
but differ in the distribution of that biomass between diameter classes
or plant types, they remain as separate entities. Thus

 is the binned above-ground biomass profile
for patch
is the binned above-ground biomass profile
for patch  ,
, is the diameter class.
is the diameter class.
 and
and  are the lower and upper
boundaries for the
are the lower and upper
boundaries for the  diameter class.
diameter class.  and
and
 depict the biomass (KgC m-2) and the number
of individuals of each cohort respectively. A difference matrix between
patches
depict the biomass (KgC m-2) and the number
of individuals of each cohort respectively. A difference matrix between
patches  and
and  is thus calculated as
is thus calculated as

If all the values of  are smaller than the
threshold,
are smaller than the
threshold, 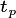 , then the patches
, then the patches  and
and  are
fused together to form a new patch
are
fused together to form a new patch 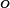 .
.
To increase computational efficiency and to simplify the coding
structure of the model, the maximum number of patches is capped at
 . To force the fusion of patches down to this number,
the simulation begins with a relatively sensitive discretization of
patches (
. To force the fusion of patches down to this number,
the simulation begins with a relatively sensitive discretization of
patches (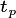 = 0.2) but if the patch number exceeds the
maximum, the fusion routine is repeated iteratively until the two most
similar patches reach their fusion threshold. This approach maintains an
even discretization along the biomass gradient, in contrast to, for
example, simply fusing the oldest or youngest patches together.
= 0.2) but if the patch number exceeds the
maximum, the fusion routine is repeated iteratively until the two most
similar patches reach their fusion threshold. This approach maintains an
even discretization along the biomass gradient, in contrast to, for
example, simply fusing the oldest or youngest patches together.
The area of the new patch ( , m
, m )
is the sum of the area of the two existing patches,
)
is the sum of the area of the two existing patches,

and the cohorts ‘belonging’ to patches  and
and  now
co-occupy patch
now
co-occupy patch  . The state properties of
. The state properties of  and
and
 (litter, seed pools, etc. ) are also averaged in accordance
with mass conservation .
(litter, seed pools, etc. ) are also averaged in accordance
with mass conservation .
1.3.3. Linked Lists: the general code structure of FATES¶
The number of patches in each natural vegetation column and the number of cohorts in any given patch are variable through time because they are re-calculated for each daily timestep of the model. The more complex an ecosystem, the larger the number of patches and cohorts. For a slowly growing ecosystem, where maximum cohort size achieved between disturbance intervals is low, the number of cohorts is also low. For fast-growing ecosystems where many plant types are viable and maximum heights are large, more cohorts are required to represent the ecosystem with adequate complexity.
In terms of variable structure, the creation of an array whose size could accommodate every possible cohort would mean defining the maximum potential number of cohorts for every potential patch, which would result in very large amounts of wasted allocated memory, on account of the heterogeneity in the number of cohorts between complex and simple ecosystems (n.b. this does still happen for some variables at restart timesteps). To resolve this, the cohort structure in FATES model does not use an array system for internal calculations. Instead it uses a system of linked lists where each cohort structure is linked to the cohorts larger than and smaller than itself using a system of pointers. The shortest cohort in each patch has a ‘shorter’ pointer that points to the null value, and the tallest cohort has a ‘taller’ pointer that points to the null value.
Instead of iterating along a vector indexed by  , the code
structures typically begin at the tallest cohort in a given patch, and
iterate until a null pointer is encountered.
, the code
structures typically begin at the tallest cohort in a given patch, and
iterate until a null pointer is encountered.
Using this structure, it is therefore possible to have an unbounded upper limit on cohort number, and also to easily alter the ordering of cohorts if, for example, a cohort of one functional type begins to grow faster than a competitor of another functional type, and the cohort list can easily be re-ordered by altering the pointer structure. Each cohort has pointers indicating to which patch and gridcell it belongs. The patch system is analogous to the cohort system, except that patches are ordered in terms of their relative age, with pointers to older and younger patches where cp is the oldest:
is the oldest:
1.3.4. Indices used in FATES¶
Some of the indices used in FATES are similar to those used in the
standard CLM4.5 model; column ( ), land unit(
), land unit( ), grid
cell(
), grid
cell( ) and soil layer (
) and soil layer ( ). On account of the
additional complexity of the new representation of plant function,
several additional indices are introduced that describe the
discritization of plant type, fuel type, litter type, plant height,
canopy identity, leaf vertical structure and fuel moisture
characteristics. To provide a reference with which to interpret the
equations that follow, they are listed here.
). On account of the
additional complexity of the new representation of plant function,
several additional indices are introduced that describe the
discritization of plant type, fuel type, litter type, plant height,
canopy identity, leaf vertical structure and fuel moisture
characteristics. To provide a reference with which to interpret the
equations that follow, they are listed here.
Parameter Symbol |
Parameter Name |
|---|---|
ft |
Plant Functional Type |
fc |
Fuel Class |
lsc |
Litter Size Class |
coh |
Cohort Index |
patch |
Patch Index |
cl |
Canopy Layer |
z |
Leaf Layer |
mc |
Moisture Class |
o |
Plant Organ Index |
s |
Nutrient Species Index |
1.3.5. Cohort State Variables¶
The unit of allometry in the ED model is the cohort. Each cohort represents a group of plants with similar functional types and heights that occupy portions of column with similar disturbance histories. The state variables of each cohort therefore consist of several pieces of information that fully describe the growth status of the plant and its position in the ecosystem structure, and from which the model can be restarted. The state variables of a cohort are as follows:
Quantity |
Variable name |
Units |
Notes |
|---|---|---|---|
Plant Functional Type |
|
integer |
|
Number of Individuals |
|
n ha-2 |
|
Height |
|
m |
|
Diameter |
|
cm |
|
Carbon Mass |
|
Kg plant-1 |
leaf, fine-root sapwood, storage, structural, reproductive |
Nutrient Mass |
|
Kg plant-1 |
Optional depending on hypothesis. See PARTEH documentation. |
Leaf memory |
|
Kg plant-1 |
Leaf mass when leaves are dropped |
Phenological Status |
|
integer |
1=leaves off. 2=leaves on |
Canopy Layer Index |
|
integer |
1=top canopy >1=understory |
Canopy trimming |
|
fraction |
1.0=max leaf area |
Patch Index |
|
integer |
To which patch does this cohort belong? |
1.3.6. Patch State Variables¶
A patch, as discuss earlier, is a fraction of the landscape which contains ecosystems with similar structure and disturbance history. A patch has no spatial location. The state variables, which are ‘ecosystem’ rather than ‘tree’ scale properties, from which the model can be restarted, are as follows
Quantity |
Variable name |
Units |
Indexed By |
|---|---|---|---|
Area |
|
m2 |
|
Age |
|
years |
|
Seed |
|
KgC m-2 |
|
Leaf Litter |
|
KgC m-2 |
|
Root Litter |
|
KgC m-2 |
|
AG Coarse Woody Debris |
|
KgC m-2 |
Size Class (lsc) |
BG Coarse Woody Debris |
|
KgC m-2 |
Size Class (lsc) |
Column Index |
|
integer |
1.3.7. Model Structure¶
Code concerned with the Ecosystem Demography model interfaces with the CLM model in four ways: i) During initialization, ii) During the calculation of surface processes (albedo, radiation absorption, canopy fluxes) each model time step (typically half-hourly), iii) During the main invokation of the ED model code at the end of each day. Daily cohort-level NPP is used to grow plants and alter the cohort structures, disturbance processes (fire and mortality) operate to alter the patch structures, and all fragmenting carbon pool dynamics are calculated. iv) during restart reading and writing. The net assimilation (NPP) fluxes attributed to each cohort are accumulated throughout each daily cycle and passed into the ED code as the major driver of vegetation dynamics.
1.4. Initialization of vegetation from bare ground¶
If the model is restarted from a bare ground state (as opposed to a
pre-existing vegetation state), the state variables above are
initialized as follows. First, the number of plants per PFT is allocated
according to the initial seeding density ( , individuals
per m
, individuals
per m ) and the area of the patch
) and the area of the patch  , which
in the first timestep is the same as the area of the notional ecosystem
, which
in the first timestep is the same as the area of the notional ecosystem
 . The model has no meaningful spatial dimension, but we
assign a notional area such that the values of ‘
. The model has no meaningful spatial dimension, but we
assign a notional area such that the values of ‘ ’ can be
attributed. The default value of
’ can be
attributed. The default value of  is one hectare (10,000
m2), but the model will behave identically irrepective of
the value of this parameter.
is one hectare (10,000
m2), but the model will behave identically irrepective of
the value of this parameter.

Each cohort is initialized at the minimum canopy height
 , which is specified as a parameter for each plant
functional type and denotes the smallest size of plant which is tracked
by the model. Smaller plants are not considered, and their emergence
from the recruitment processes is unresolved and therefore implicitly
parameterized in the seedling establishment model.
, which is specified as a parameter for each plant
functional type and denotes the smallest size of plant which is tracked
by the model. Smaller plants are not considered, and their emergence
from the recruitment processes is unresolved and therefore implicitly
parameterized in the seedling establishment model.
The diameter of each cohort is then specified according to the height-diameter allometry function associated with the PFT of interest, see Table of Allometric Functions. The biomass pools for the newly recruited plant are then determined from the allometry equations that define the target (idealized) sizes for each pool.
Parameter Symbol |
Parameter Name |
Units |
Default Value |
|---|---|---|---|
|
Minimum plant height |
m |
1.5 |
|
Initial Planting density |
Individuals m-2 |
1.5. Allocation and Reactive Transport (PARTEH)¶
The Plant Allocation and Reactive Transport Extensible Hypotheses (PARTEH) is a suite of modules that handle the processes of allocation, transport and reactions (i.e. thos processes related to movement and change, yet perhaps not the genesis) of various arbitrary species (carbon, nutrients, toxins, etc) within the various organs of live vegetation. In FATES, these processes are resolved per unit plant, for each cohort.
1.6. Allometry and Growth Along Allometric Curves¶
In the previous section, Allocation and Reactive Transport (PARTEH), we covered the equations that describe how growth is implemented, as well the order of operations and logic of that forumlation. In this section, we will discuss the various allometric functions that generate the relative rates of change, as well as the target biomass quantities  .
.
1.6.1. “Forced” Growth Along Allometric Curves¶
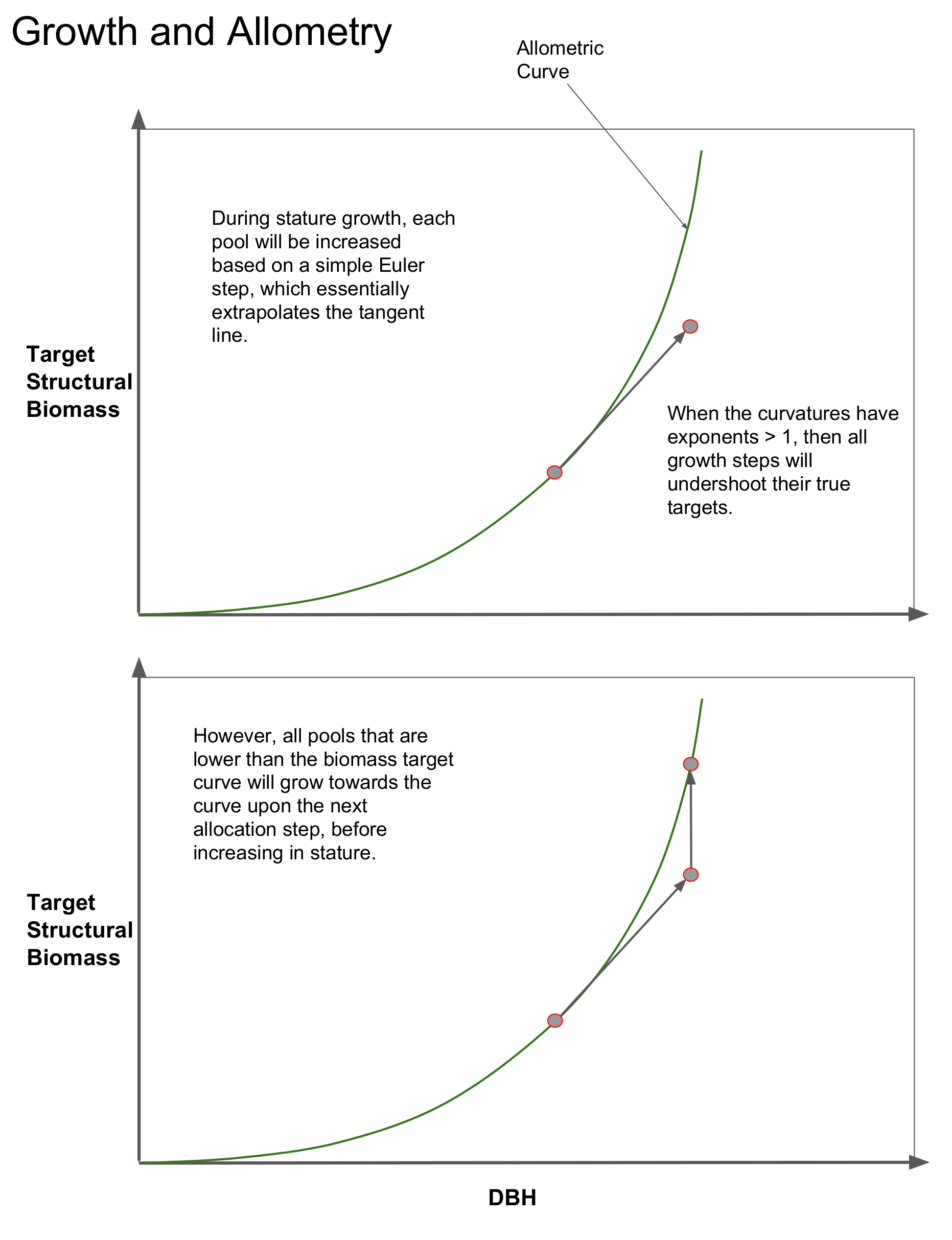
Growth specified by current PARTEH hypotheses follow along the allometric curves. A hypothetical example of a cohorts integration along such a curve is provided in the top panel of the diagram below. It is assumed that when a plant grows in stature, the structural biomass matches the target structural biomass for its size (DBH). This is represented by the grey dot sitting on the allometry line for structural biomass.
A state of being “on allometry” is consistent with the cohort (grey dot) existing on the allometric curve.
It is expected, and it is represented in the model, that due to either continuous or event based turnover, that biomass pools are continually depleted, thus pulling the grey dot straight down, away from the allometry line. Recall from the PARTEH description, that the first step in the growth algorithm is to use available carbon to replace these lost biomass pools (without increasing dbh) so that it is “on allometry”.
Also, all numerical integration has some amount of truncation error (step error). When FATES conducts the stature growth integration step, it typically uses Euler integration, because it is fast and simple. As a result, all biomass pools are projected along the tangent of the allometric curves from where they started. When the curvature parameters that govern these relationships are greater than 1, this results in continual “undershooting” of the actual target quantity. This is not a liability, firstly because growth is forced to be mass conservative. And secondly, to re-iterate the explanation above, upon the next growth step the algorithm will spend carbon to first get the pools back “on allometry”, before it projects along the tangent again. This is represented in the lower panel.
However, we also have to accomodate for cases where the actual amount of biomass in the cohort’s pools are larger than the target sizes dictated by the cohort’s diameter. This can be visualized by the cohort residing somewhere above the line. This can happen for two reasons, 1) cohort fusion or 2) growth along allometric curves with curvature parameters (exponents) less than 1.
For woody plants, if a non-structural biomass pool is greater than the target pool size, the solution is simple. That pool is flagged to be ignored during the stature growth step, and eventually the cohort’s dbh will increase such that the target size exceeds its actual size again. This is visualized in the top panel of the diagram below.
There is a caveat here. The diameter must be “tied” to one of the biomass pools. And for woody plants, we choose structural carbon. And thus, we cannot flag to ignore structural carbon during stature growth since it is inextricably linked to diameter. Therefore, cohorts that have structural biomass that is greater than the target biomass dictated by its diameter, will have their DBH forceably increased (without increasing any biomass) until the allometric target matches the actual biomass. See the lower panel in the diagram below.
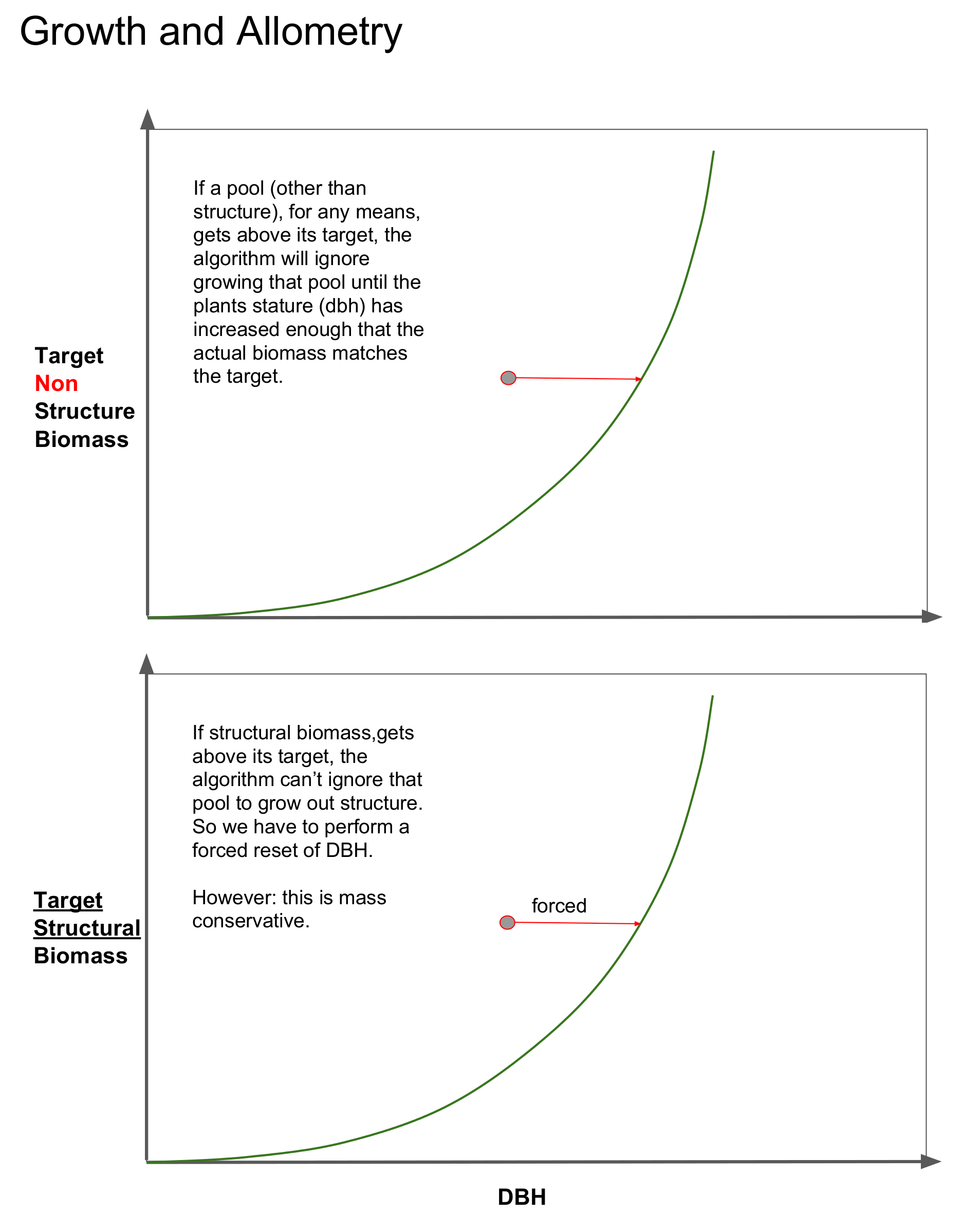
Note, the explanation above was explained for woody plants, which tie diameter to structural biomass. For non-woody plants, such as grasses, we tie leaf biomass to diameter instead.
1.6.2. Allometric Relationships¶
FATES-PARTEH (in its base hypotheses) uses allometry to dictate the target biomass quantities of structure, sapwood, leaf, fine-root, reproduction and storage. Further, FATES also uses allometric relationships to define a cohort’s height and crown area. All of these target quantities are tied to diameter. Biomass pools may also be functionally dependent on other biomass pools, as long as a cyclical relationship is not generated, and can ultimately be related to diameter or other external factors. For instance, target root biomass is typically defined as proportional to leaf biomass. Target leaf biomass is dependent on height and a canopy trimming function, while crown area and above ground biomass are each also dependent on height.
The FATES code is written in a way that offers flexibility in how these relationships are cast. Each of these forumulations uses one or more user defined constant parameters, but it also allows for completely different functional forms. All of FATES allometric relationships can be found in the file FatesAllometryMod.F90.
Important note. Most allometry relationships from field research define total above ground biomass (AGB) as their estimated quantity instead of structural biomass. In FATES, since AGB is not a state-variable, it must be derived from the portions of several state variables. However, we make a simplification in FATES, and assume that the allometric relationships for AGB only contain structural wood and sapwood, and do not contain leaves, storage or reproductive tissues. Diagnostics on AGB will include all terms. Thus the allometric target for AGB contains the state targets and the fraction of above ground biomass (pft constant parameter)  .
.
(1.45)¶
Note that the diameter to height relationships all use an effective diameter,  . This is the minimum between the actual plant diameter, and the PFT specific parameter that specifies the diameter at which maximum height occurs
. This is the minimum between the actual plant diameter, and the PFT specific parameter that specifies the diameter at which maximum height occurs 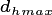 .
.
(1.46)¶
The following table details the different allometric relationships that governs growth and stature, and the optional relationships and parameters associated with those relationships.
Reference |
Function |
|---|---|
Diameter to Height |
|
Power Function |
|
|
|
|
|
|
|
Target Above Ground Biomass |
|
|
|
2 Parameter power function |
|
|
|
Target Leaf Biomass (TBD) |
|
Target Sapwood Biomass (TBD) |
|
Target Fine-root Biomass (TBD) |
|
Target Storage Biomass (TBD) |
|
List of allometric relationships, their functional forms, and relevant parameters.
1.7. Canopy Structure and the Perfect Plasticity Approximation¶
During initialization and every subsequent daily ED timestep, the canopy structure model is called to determine how the leaf area of the different cohorts is arranged relative to the incoming radiation, which will then be used to drive the radiation and photosynthesis calculations. This task requires that some assumptions are made about 1) the shape and depth of the canopy within which the plant leaves are arranged and 2) how the leaves of different cohorts are arranged relative to each other. This set of assumptions are critical to model performance in ED-like cohort based models, since they determine how light resources are partitioned between competing plants of varying heights, which has a very significant impact on how vegetation distribution emerges from competition Fisher et al. 2010.
The standard ED1.0 model makes a simple ‘flat disk’ assumption, that the leaf area of each cohort is spread in an homogenous layer at one exact height across entire the ground area represented by each patch. FATES has diverged from this representation due to (at least) two problematic emergent properties that we identified as generating unrealistic behaviours espetially for large-area patches.
1. Over-estimation of light competition . The vertical stacking of cohorts which have all their leaf area at the same nominal height means that when one cohort is only very slightly taller than it’s competitor, it is completely shaded by it. This means that any small advantage in terms of height growth translates into a large advantage in terms of light competition, even at the seedling stage. This property of the model artificially exaggerates the process of light competition. In reality, trees do not compete for light until their canopies begin to overlap and canopy closure is approached.
2. Unrealistic over-crowding. The ‘flat-disk’ assumption has no consideration of the spatial extent of tree crowns. Therefore it has no control on the packing density of plants in the model. Given a mismatch between production and mortality, entirely unrealistic tree densities are thus possible for some combinations of recruitment, growth and mortality rates.
To account for the filling of space in three dimensions using the one-dimensional representation of the canopy employed by CLM, we implement a new scheme derived from that of Purves et al. 2008. Their argument follows the development of an individual-based variant of the SORTIE model, called SHELL, which allows the location of individual plant crowns to be highly flexible in space. Ultimately, the solutions of this model possess an emergent property whereby the crowns of the plants simply fill all of the available space in the canopy before forming a distinct understorey.
Purves et al. developed a model that uses this feature, called the
‘perfect plasticity approximation’, which assumes the plants are able to
perfectly fill all of the available canopy space. That is, at canopy
closure, all of the available horizontal space is filled, with
negligible gaps, owing to lateral tree growth and the ability of tree
canopies to grow into the available gaps (this is of course, an
over-simplified but potential useful ecosystem property). The ‘perfect
plasticity approximation’ (PPA) implies that the community of trees is
subdivided into discrete canopy layers, and by extension, each cohort
represented by FATES model is assigned a canopy layer status flag,
 . In this version, we set the maximum number of canopy layers
at 2 for simplicity, although is possible to have a larger number of
layers in theory.
. In this version, we set the maximum number of canopy layers
at 2 for simplicity, although is possible to have a larger number of
layers in theory. 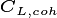 = 1 means that all the trees of
cohort
= 1 means that all the trees of
cohort  are in the upper canopy (overstory), and
are in the upper canopy (overstory), and
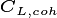 = 2 means that all the trees of cohort
= 2 means that all the trees of cohort  are
in the understorey.
are
in the understorey.
In this model, all the trees in the canopy experience full light on their uppermost leaf layer, and all trees in the understorey experience the same light (full sunlight attenuated by the average LAI of the upper canopy) on their uppermost leaves, as described in the radiation transfer section (more nuanced versions of this approach may be investigated in future model versions). The canopy is assumed to be cylindrical, the lower layers of which experience self-shading by the upper layers.
To determine whether a second canopy layer is required, the model needs
to know the spatial extent of tree crowns. Crown area,
 , m2, is defined as
, m2, is defined as

where  is the crown area of a single tree canopy
(m2) and
is the crown area of a single tree canopy
(m2) and  is the ‘canopy spread’
parameter (unitless), which is assigned as a
function of canopy space filling, discussed below.
is the ‘canopy spread’
parameter (unitless), which is assigned as a
function of canopy space filling, discussed below.  is effectively
a normalisation constant in the power law describing the relationship of crown area
to dbh. However, this is not constant but varies by the canopy areae to ground area fraction.
In contrast to
Purves et al. 2008 , by default we use an exponent, identical to that
for leaf biomass,
is effectively
a normalisation constant in the power law describing the relationship of crown area
to dbh. However, this is not constant but varies by the canopy areae to ground area fraction.
In contrast to
Purves et al. 2008 , by default we use an exponent, identical to that
for leaf biomass,  , not 2.0, such that tree leaf area index does
not change as a function of diameter. The option is also available to modify
the exponent using the difference parameter,
, not 2.0, such that tree leaf area index does
not change as a function of diameter. The option is also available to modify
the exponent using the difference parameter,  .
.
To determine whether the canopy is closed, we calculate the total canopy area as:
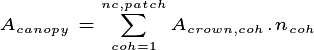
where  is the number of cohorts in a given patch. If
the area of all crowns
is the number of cohorts in a given patch. If
the area of all crowns  (m2) is larger
than the total ground area of a patch (
(m2) is larger
than the total ground area of a patch ( ), which
typically happens at the end of the day, after growth and updated crown
allometry is resolved in the model, then some
fraction of each cohort is demoted to the understorey.
), which
typically happens at the end of the day, after growth and updated crown
allometry is resolved in the model, then some
fraction of each cohort is demoted to the understorey.
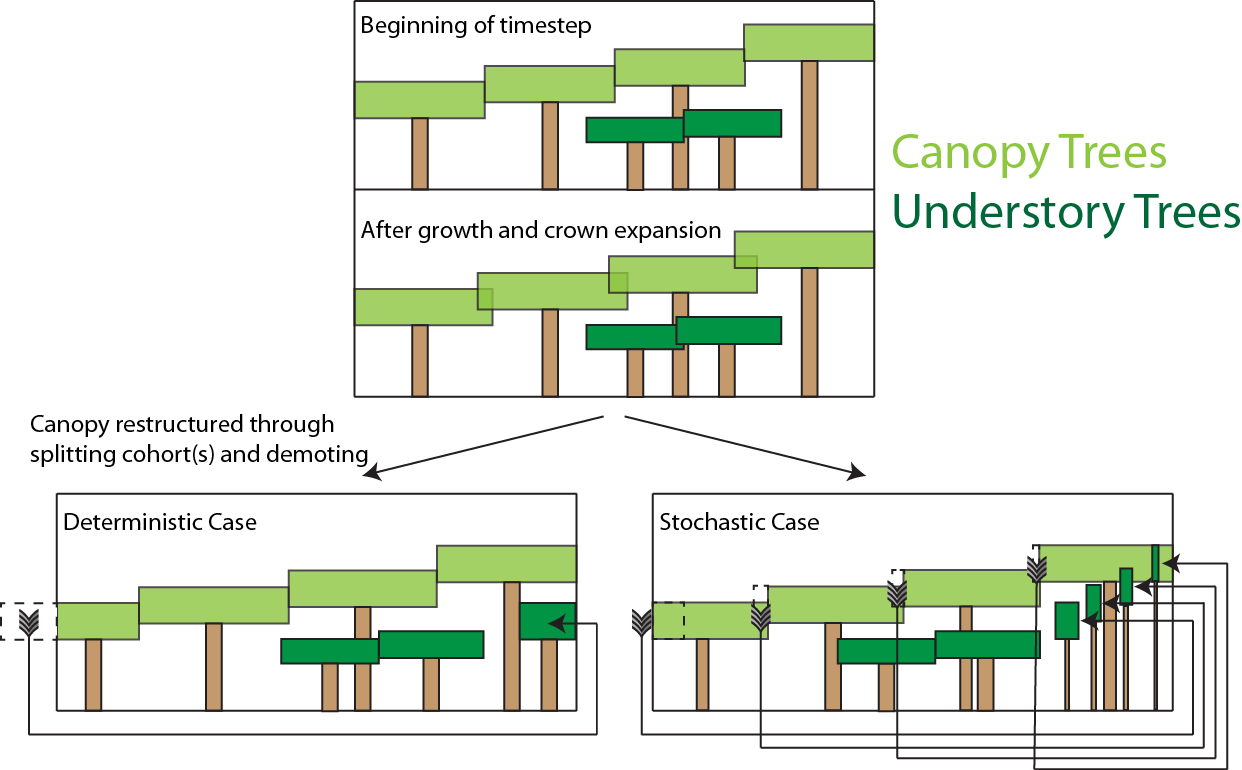
Under these circumstances, the extra crown area  (i.e.,
(i.e.,  -
-  ) is moved into the understorey.
For each cohort already in the canopy, we determine a fraction of trees
that are moved from the canopy (
) is moved into the understorey.
For each cohort already in the canopy, we determine a fraction of trees
that are moved from the canopy ( ) to the understorey.
) to the understorey.
 is calculated as Fisher et al. 2010
is calculated as Fisher et al. 2010
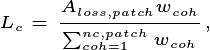
where  is a weighting of each cohort. There are two possible ways of calculating this weighting coefficient. The first, as described in Fisher et al. 2010, is to probabilistically weight cohorts based on their height
is a weighting of each cohort. There are two possible ways of calculating this weighting coefficient. The first, as described in Fisher et al. 2010, is to probabilistically weight cohorts based on their height  (m) and the competitive exclusion coefficient
(m) and the competitive exclusion coefficient


The higher the value of  the greater the impact of tree
diameter on the probability of a given tree obtaining a position in the
canopy layer. That is, for high
the greater the impact of tree
diameter on the probability of a given tree obtaining a position in the
canopy layer. That is, for high  values, competition is
highly deterministic. The smaller the value of
values, competition is
highly deterministic. The smaller the value of  , the greater
the influence of random factors on the competitive exclusion process,
and the higher the probability that slower growing trees will get into
the canopy. Appropriate values of
, the greater
the influence of random factors on the competitive exclusion process,
and the higher the probability that slower growing trees will get into
the canopy. Appropriate values of  are poorly constrained but
alter the outcome of competitive processes.
are poorly constrained but
alter the outcome of competitive processes.
The second way of weighting the cohorts is a more determinstic method based on a strict rank-ordering of the cohorts by height, where all cohorts shorter than that cohorts whose cumulative (from the tallest cohort) rank-ordered crown area equals the area of the patch area are demoted to the lower canopy layer. This is derived from the original PPA algorithm described in Purves et al. 2008.
The process by which trees are moved between canopy layers is complex
because 1) the crown area predicted for a cohort to lose may be larger
than the total crown area of the cohort, which requires iterative
solutions, and 2) on some occasions (e.g. after fire, or if the parameter which sets the disturbed area as a function of the fractional crown area of canopy tree mortality is less than one), the canopy may
open up and require ‘promotion’ of cohorts from the understorey, and 3)
canopy area may change due to the variations of canopy spread values ( , see the section below for details) when
fractions of cohorts are demoted or promoted. Further details can be
found in the code references in the footnote.
, see the section below for details) when
fractions of cohorts are demoted or promoted. Further details can be
found in the code references in the footnote.
1.7.1. Horizontal Canopy Spread¶
Purves et al. 2008 estimated the ratio between canopy and
stem diameter 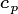 as 0.1 m cm-1 for canopy trees
in North American forests, but this estimate was made on trees in closed
canopies, whose shape is subject to space competition from other
individuals. Sapling trees have no constraints in their horizontal
spatial structure, and as such, are more likely to display their leaves
to full sunlight. Also, prior to canopy closure, light interception by
leaves on the sides of the canopy is also higher than it would be in a
closed canopy forest. If the ‘canopy spread’ parameter is constant for
all trees, then we simulate high levels of self-shading for plants in
unclosed canopies, which is arguably unrealistic and can lower the
productivity of trees in areas of unclosed canopy (e.g. low productivity
areas of boreal or semi-arid regions where LAI and canopy cover might
naturally be low). We here interpret the degree of canopy spread,
as 0.1 m cm-1 for canopy trees
in North American forests, but this estimate was made on trees in closed
canopies, whose shape is subject to space competition from other
individuals. Sapling trees have no constraints in their horizontal
spatial structure, and as such, are more likely to display their leaves
to full sunlight. Also, prior to canopy closure, light interception by
leaves on the sides of the canopy is also higher than it would be in a
closed canopy forest. If the ‘canopy spread’ parameter is constant for
all trees, then we simulate high levels of self-shading for plants in
unclosed canopies, which is arguably unrealistic and can lower the
productivity of trees in areas of unclosed canopy (e.g. low productivity
areas of boreal or semi-arid regions where LAI and canopy cover might
naturally be low). We here interpret the degree of canopy spread,
 as a function of how much tree crowns interfere with each
other in space, or the total canopy area
as a function of how much tree crowns interfere with each
other in space, or the total canopy area  . However
. However
 itself is a function of
itself is a function of  , leading to a
circularity.
, leading to a
circularity.  is thus solved iteratively through time.
is thus solved iteratively through time.
Each daily model step,  and the fraction of the
gridcell occupied by tree crowns in the top canopy layer
is calculated (based on
and the fraction of the
gridcell occupied by tree crowns in the top canopy layer
is calculated (based on  from the previous timestep):
from the previous timestep):
( =
=  /
/ )
)
If  is greater than a threshold value
is greater than a threshold value  ,
,
 is increased by a small increment
is increased by a small increment 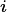 , where
, where  (see bleow for definitions).
The threshold
(see bleow for definitions).
The threshold  is, hypothetically, the canopy fraction at which light
competition begins to impact on tree growth. This is less than 1.0 owing
to the non-perfect spatial spacing of tree canopies. If
is, hypothetically, the canopy fraction at which light
competition begins to impact on tree growth. This is less than 1.0 owing
to the non-perfect spatial spacing of tree canopies. If  is greater than
is greater than  , then
, then  is reduced by an
increment
is reduced by an
increment 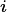 , to reduce the spatial extent of the canopy, thus.
, to reduce the spatial extent of the canopy, thus.

The values of  are bounded to upper and lower limits. The
lower limit corresponds to the observed canopy spread parameter for
canopy trees
are bounded to upper and lower limits. The
lower limit corresponds to the observed canopy spread parameter for
canopy trees  and the upper limit corresponds to the
largest canopy extent
and the upper limit corresponds to the
largest canopy extent 

This iterative scheme requires two additional parameters ( and
and
 ).
).  takes a value between 0 and 1 and affects the
speed with which canopy spread,
takes a value between 0 and 1 and affects the
speed with which canopy spread,  changes.
However, the model is relatively insensitive to the choice of either
changes.
However, the model is relatively insensitive to the choice of either
 or
or  .
.
1.7.2. Definition of Leaf and Stem Area Profile¶
Within each patch, the model defines and tracks cohorts of multiple plant functional types that exist either in the canopy or understorey. Light on the top leaf surface of each cohort in the canopy is the same, and the rate of decay through the canopy is also the same for each PFT. Therefore, we accumulate all the cohorts of a given PFT together for the sake of the radiation and photosynthesis calculations (to avoid separate calculations for every cohort).
Therefore, the leaf area index for each patch is defined as a
three-dimensional array  where
where 
is the canopy layer, 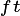 is the functional type and
is the functional type and  is
the leaf layer within each canopy. This three-dimensional structure is
the basis of the radiation and photosynthetic models. In addition to a
leaf area profile matrix, we also define, for each patch, the area which
is covered by leaves at each layer as
is
the leaf layer within each canopy. This three-dimensional structure is
the basis of the radiation and photosynthetic models. In addition to a
leaf area profile matrix, we also define, for each patch, the area which
is covered by leaves at each layer as  .
.
Each plant cohort is already defined as a member of a single canopy
layer and functional type. This means that to generate the
 matrix, it only remains to divide the leaf area of
each cohort into leaf layers. First, we determine how many leaf layers
are occupied by a single cohort, by calculating the ‘tree LAI’ as the
total leaf area of each cohort divided by its crown area (both in
m2)
matrix, it only remains to divide the leaf area of
each cohort into leaf layers. First, we determine how many leaf layers
are occupied by a single cohort, by calculating the ‘tree LAI’ as the
total leaf area of each cohort divided by its crown area (both in
m2)

where  is the specific leaf area in
m2 KgC-1 and
is the specific leaf area in
m2 KgC-1 and  is in KgC per plant.
is in KgC per plant.
Stem area index (SAI) is ratio of the total area of all woody stems on a plant to the area of ground covered by the plant. During winter in deciduous areas, the extra absorption by woody stems can have a significant impact on the surface energy budget. However, in previous big leaf versions of the CLM, computing the circumstances under which stem area was visible in the absence of leaves was difficult and the algorithm was largely heuristic as a result. Given the multi-layer canopy introduced for FATES, we can determine the leaves in the higher canopy layers will likely shade stem area in the lower layers when leaves are on, and therefore stem area index can be calculated as a function of woody biomass directly.
Literature on stem area index is particularly poor, as it’s estimation
is complex and not particularly amenable to the use of, for example,
assumptions of random distribution in space that are typically used to
calculate leaf area from light interception.
Kucharik et al. 1998 estimated that SAI visible from an
LAI2000 sensor was around 0.5 m2 m-2. Low et al. 2001
estimate that the wood area index for Ponderosa Pine forest is
0.27-0.33. The existing CLM(CN) algorithm sets the minimum SAI at 0.25
to match MODIS observations, but then allows SAI to rise as a function
of the LAI lost, meaning than in some places, predicted SAI can reach
value of 8 or more. Clearly, greater scientific input on this quantity
is badly needed. Here we determine that SAI is a linear function of
woody biomass, to at very least provide a mechanistic link between the
existence of wood and radiation absorbed by it. The non-linearity
between how much woody area exists and how much radiation is absorbed is
provided by the radiation absorption algorithm. Specifically, the SAI of
an individual cohort ( , m2
m-2) is calculated as follows,
, m2
m-2) is calculated as follows,

where  is the coefficient linking structural biomass to
SAI. The number of occupied leaf layers for cohort
is the coefficient linking structural biomass to
SAI. The number of occupied leaf layers for cohort  (
( ) is then equal to the rounded up integer value of the
tree SAI (
) is then equal to the rounded up integer value of the
tree SAI ( ) and LAI (
) and LAI ( )
divided by the layer thickness (i.e., the resolution of the canopy layer
model, in units of vegetation index (
)
divided by the layer thickness (i.e., the resolution of the canopy layer
model, in units of vegetation index ( +
+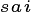 ) with a
default value of 1.0,
) with a
default value of 1.0, 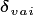 ),
),

The fraction of each layer that is leaf (as opposed to stem) can then be calculated as

Finally, the leaf area in each leaf layer pertaining to this cohort is thus

and the stem area index is

where  is the remainder of the canopy that is below the
last full leaf layer
is the remainder of the canopy that is below the
last full leaf layer
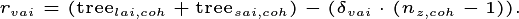
 is the total canopy area occupied by plants in
a given patch (m:math:^{2}) and is calculated as follows,
is the total canopy area occupied by plants in
a given patch (m:math:^{2}) and is calculated as follows,

The canopy is conceived as a cylinder, although this assumption could be
altered given sufficient evidence that canopy shape was an important
determinant of competitive outcomes, and the area of ground covered by
each leaf layer is the same through the cohort canopy. With the
calculated SAI and LAI, we are able to calculate the complete canopy
profile. Specifically, the relative canopy area for the cohort
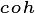 is calculated as
is calculated as

The total occupied canopy area for each canopy layer ( ), plant
functional type (
), plant
functional type (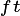 ) and leaf layer (
) and leaf layer ( ) bin is thus
) bin is thus

where  and
and 
All of these quantities are summed across cohorts to give the complete leaf and stem area profiles,


1.7.3. Burial of leaf area by snow¶
The calculations above all pertain to the total leaf and stem area
indices which charecterize the vegetation structure. In addition, the
model must know when the vegetation is covered by snow, and by how much,
so that the albedo and energy balance calculations can be adjusted
accordingly. Therefore, we calculated a ‘total’ and ‘exposed’
 and
and 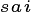 profile using a representation of the bottom
and top canopy heights, and the depth of the average snow pack. For each
leaf layer
profile using a representation of the bottom
and top canopy heights, and the depth of the average snow pack. For each
leaf layer  of each cohort, we calculate an ‘exposed fraction
of each cohort, we calculate an ‘exposed fraction
 via consideration of the top and bottom heights of
that layer
via consideration of the top and bottom heights of
that layer 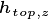 and
and  (m),
(m),

where  is the plant functional type (
is the plant functional type (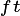 )
specific fraction of the cohort height that is occupied by the crown.
Specifically, the ‘exposed fraction
)
specific fraction of the cohort height that is occupied by the crown.
Specifically, the ‘exposed fraction  is calculated as
follows,
is calculated as
follows,

The resulting exposed ( ) and total
(
) and total
( ) leaf and stem area indicies are calculated as
) leaf and stem area indicies are calculated as

and are used in the radiation interception and photosynthesis algorithms described later.
Parameter Symbol |
Parameter Name |
Units |
Notes |
Indexed by |
|---|---|---|---|---|
|
Thickness of single canopy layer |
m2 m-2 |
||
|
Competitive Exclusion Parameter |
none |
||
|
Minimum canopy spread |
m2 cm-1 |
||
|
Competitive Exclusion Parameter |
m2 cm-1 |
||
|
Incremental
change in
|
m2 cm-1 y-1 |
||
|
Threshold canopy closure |
none |
||
|
Crown fraction |
none |
|
|
|
Stem area per unit woody biomass |
m2 KgC-1 |
1.8. Radiation Transfer¶
1.8.1. Fundamental Radiation Transfer Theory¶
The first interaction of the land surface with the properties of vegetation concerns the partitioning of energy into that which is absorbed by vegetation, reflected back into the atmosphere, and absorbed by the ground surface. Older versions of the CLM have utilized a “two-stream” approximation Sellers 1985, Sellers et al. 1986 that provided an empirical solution for the radiation partitioning of a multi-layer canopy for two streams, of diffuse and direct light. However, implementation of the Ecosystem Demography model requires a) the adoption of an explicit multiple layer canopy b) the implementation of a multiple plant type canopy and c) the distinction of canopy and under-storey layers, in-between which the radiation streams are fully mixed. The radiation mixing between canopy layers is necessary as the position of different plants in the under-storey is not defined spatially or relative to the canopy trees above. In this new scheme, we thus implemented a one-dimensional scheme that traces the absorption, transmittance and reflectance of each canopy layer and the soil, iterating the upwards and downwards passes of radiation through the canopy until a pre-defined accuracy tolerance is reached. This approach is based on the work of Norman 1979.
Here we describe the basic theory of the radiation transfer model for
the case of a single homogenous canopy, and in the next section we
discuss how this is applied to the multi layer multi PFT canopy in the
FATES implementation. The code considers the fractions of a single
unit of incoming direct and a single unit of incoming diffuse light,
that are absorbed at each layer of the canopy for a given solar angle
( , radians). Direct radiation is extinguished through
the canopy according to the coefficient
, radians). Direct radiation is extinguished through
the canopy according to the coefficient  that is
calculated from the incoming solar angle and the dimensionless leaf
angle distribution parameter (
that is
calculated from the incoming solar angle and the dimensionless leaf
angle distribution parameter ( ) as
) as

where

and

The leaf angle distribution is a descriptor of how leaf surfaces are arranged in space. Values approaching 1.0 indicate that (on average) the majority of leaves are horizontally arranged with respect to the ground. Values approaching -1.0 indicate that leaves are mostly vertically arranged, and a value of 0.0 denotes a canopy where leaf angle is random (a ‘spherical’ distribution).
According to Beer’s Law, the fraction of light that is transferred
through a single layer of vegetation (leaves or stems) of thickness
 , without being intercepted by any surface, is
, without being intercepted by any surface, is

and the incident direct radiation transmitted to each layer of the
canopy ( ) is thus calculated from the cumulative leaf
area (
) is thus calculated from the cumulative leaf
area (  ) shading each layer (
) shading each layer ( ):
):

The fraction of the leaves  that are exposed to direct
light is also calculated from the decay coefficient
that are exposed to direct
light is also calculated from the decay coefficient  .
.

where  is the fraction of leaves that are shaded
from direct radiation and only receive diffuse light.
is the fraction of leaves that are shaded
from direct radiation and only receive diffuse light.
Diffuse radiation, by definition, enters the canopy from a spectrum of
potential incident directions, therefore the un-intercepted transfer
( ) through a leaf layer of thickness
) through a leaf layer of thickness  is
calculated as the mean of the transfer rate from each of 9 different
incident light directions (
is
calculated as the mean of the transfer rate from each of 9 different
incident light directions ( ) between 0 and 180 degrees
to the horizontal.
) between 0 and 180 degrees
to the horizontal.


The fraction (1- ) of the diffuse radiation is
intercepted by leaves as it passes through each leaf layer. Of this,
some fraction is reflected by the leaf surfaces and some is transmitted
through. The fractions of diffuse radiation reflected from
(
) of the diffuse radiation is
intercepted by leaves as it passes through each leaf layer. Of this,
some fraction is reflected by the leaf surfaces and some is transmitted
through. The fractions of diffuse radiation reflected from
( ) and transmitted though
(
) and transmitted though
( ) each layer of leaves are thus,
respectively
) each layer of leaves are thus,
respectively

where  and
and  are the fractions of
incident light reflected and transmitted by individual leaf surfaces.
are the fractions of
incident light reflected and transmitted by individual leaf surfaces.
Once we know the fractions of light that are transmitted and reflected
by each leaf layer, we begin the process of distributing light through
the canopy. Starting with the first leaf layer ( =1), where
the incident downwards diffuse radiation (
=1), where
the incident downwards diffuse radiation ( )
is 1.0, we work downwards for
)
is 1.0, we work downwards for  layers, calculating the
radiation in the next layer down (
layers, calculating the
radiation in the next layer down ( ) as:
) as:

Here,  calculates the
fraction of incoming energy transmitted downwards onto layer
calculates the
fraction of incoming energy transmitted downwards onto layer
 . This flux is then increased by the additional radiation
. This flux is then increased by the additional radiation
 that is reflected upwards from further down in the canopy to
layer
that is reflected upwards from further down in the canopy to
layer  , and then is reflected back downwards according to the
reflected fraction
, and then is reflected back downwards according to the
reflected fraction  . The more radiation in
. The more radiation in
 , the smaller the
denominator and the larger the downwards flux.
, the smaller the
denominator and the larger the downwards flux. 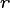 is also
calculated sequentially, starting this time at the soil surface layer
(where
is also
calculated sequentially, starting this time at the soil surface layer
(where  )
)

where  is the soil albedo characteristic. The upwards
reflected fraction
is the soil albedo characteristic. The upwards
reflected fraction  for each leaf layer, moving upwards, is
then Norman 1979
for each leaf layer, moving upwards, is
then Norman 1979

The corresponding upwards diffuse radiation flux is therefore the fraction of downwards radiation that is incident on a particular layer, multiplied by the fraction that is reflected from all the lower layers:

Now we have initial conditions for the upwards and downwards diffuse
fluxes, these must be modified to account for the fact that, on
interception with leaves, direct radiation is transformed into diffuse
radiation. In addition, the initial solutions to the upwards and
downwards radiation only allow a single ‘bounce’ of radiation through
the canopy, so some radiation which might be intercepted by leaves
higher up is potentially lost. Therefore, the solution to this model is
iterative. The iterative solution has upwards and a downwards components
that calculate the upwards and downwards fluxes of total radiation at
each leaf layer ( and
and  ) . The
downwards component begins at the top canopy layer (
) . The
downwards component begins at the top canopy layer ( ). Here
we define the incoming solar diffuse and direct radiation
(
). Here
we define the incoming solar diffuse and direct radiation
( and
and  respectively).
respectively).

The first term of the right-hand side deals with the diffuse radiation
transmitted downwards, the second with the diffuse radiation travelling
upwards, and the third with the direct radiation incoming at each layer
( ) that is intercepted by leaves
(
) that is intercepted by leaves
( ) and then transmitted through through the leaf
matrix as diffuse radiation (
) and then transmitted through through the leaf
matrix as diffuse radiation (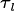 ). At the bottom of the
canopy, the light reflected off the soil surface is calculated as
). At the bottom of the
canopy, the light reflected off the soil surface is calculated as

The upwards propagation of the reflected radiation is then

Here the first two terms deal with the diffuse downwards and upwards
fluxes, as before, and the third deals direct beam light that is
intercepted by leaves and reflected upwards. These upwards and downwards
fluxes are computed for multiple iterations, and at each iteration,
 and
and 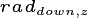 are compared to their
values in the previous iteration. The iteration scheme stops once the
differences between iterations for all layers is below a predefined
tolerance factor, (set here at
are compared to their
values in the previous iteration. The iteration scheme stops once the
differences between iterations for all layers is below a predefined
tolerance factor, (set here at  ). Subsequently, the
fractions of absorbed direct (
). Subsequently, the
fractions of absorbed direct ( ) and diffuse
(
) and diffuse
( ) radiation for each leaf layer then
) radiation for each leaf layer then


and, the radiation energy absorbed by the soil for the diffuse and direct streams is is calculated as

Canopy level albedo is denoted as the upwards flux from the top leaf layer

and the division of absorbed energy into sunlit and shaded leaf fractions, (required by the photosynthesis calculations), is


1.8.2. Resolution of radiation transfer theory within the FATES canopy structure¶
The radiation transfer theory above, was described with reference to a
single canopy of one plant functional type, for the sake of clarity of
explanation. The FATES model, however, calculates radiative and
photosynthetic fluxes for a more complex hierarchical structure within
each patch/time-since-disturbance class, as described in the leaf area
profile section. Firstly, we denote two or more canopy layers (denoted
 ). The concept of a ‘canopy layer’ refers to the idea that
plants are organized into discrete over and under-stories, as predicted
by the Perfect Plasticity Approximation
(Purves et al. 2008, Fisher et al. 2010). Within each canopy layer
there potentially exist multiple cohorts of different plant functional
types and heights. Within each canopy layer,
). The concept of a ‘canopy layer’ refers to the idea that
plants are organized into discrete over and under-stories, as predicted
by the Perfect Plasticity Approximation
(Purves et al. 2008, Fisher et al. 2010). Within each canopy layer
there potentially exist multiple cohorts of different plant functional
types and heights. Within each canopy layer,  , and functional
type,
, and functional
type, 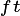 , the model resolves numerous leaf layers
, the model resolves numerous leaf layers  ,
and, for some processes, notably photosynthesis, each leaf layer is
split into a fraction of sun and shade leaves,
,
and, for some processes, notably photosynthesis, each leaf layer is
split into a fraction of sun and shade leaves,  and
and
 , respectively.
, respectively.
The radiation scheme described in Section is solved explicitly for this structure, for both the visible and near-infrared wavebands, according to the following assumptions.
A canopy layer (
 ) refers literally to the vertical layer
within the canopy this cohort resides in. The top canopy layer
has index 1. A closed canopy forest will therefore by definition
have at least two layers, and perhaps more.
) refers literally to the vertical layer
within the canopy this cohort resides in. The top canopy layer
has index 1. A closed canopy forest will therefore by definition
have at least two layers, and perhaps more.A leaf layer (
 ) refers to the discretization of the LAI
within the canopy of a given plant functional type.
) refers to the discretization of the LAI
within the canopy of a given plant functional type.All PFTs in the same canopy layer have the same solar radiation incident on the top layer of the canopy
Light is transmitted through the canopy of each plant functional type independently
Between canopy layers, the light streams from different plant functional types are mixed, such that the (undefined) spatial location of plants in lower canopy layers does not impact the amount of light received.
Where understorey layers fill less area than the overstorey layers, radiation is directly transferred to the soil surface.
All these calculations pertain to a single patch, so we omit the patch subscript for simplicity in the following discussion.
Within this framework, the majority of the terms in the radiative
transfer scheme are calculated with indices of  ,
,
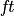 and
and  . In the following text, we revisit the
simplified version of the radiation model described above, and explain
how it is modified to account for the more complex canopy structure used
by FATES.
. In the following text, we revisit the
simplified version of the radiation model described above, and explain
how it is modified to account for the more complex canopy structure used
by FATES.
Firstly, the light penetration functions,  and
and
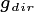 are described as functions of
are described as functions of 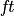 , because
the leaf angle distribution,
, because
the leaf angle distribution,  , is a pft-specific
parameter. Thus, the diffuse irradiance transfer rate,
, is a pft-specific
parameter. Thus, the diffuse irradiance transfer rate,  is also
is also 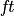 specific because
specific because 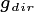 , on which it
depends, is a function of
, on which it
depends, is a function of  .
.
The amount of direct light reaching each leaf layer is a function of the
leaves existing above the layer in question. If a leaf layer ‘ ’
is in the top canopy layer (the over-storey), it is only shaded by
leaves of the same PFT so
’
is in the top canopy layer (the over-storey), it is only shaded by
leaves of the same PFT so  is unchanged from equation. If
there is more than one canopy layer (
is unchanged from equation. If
there is more than one canopy layer ( ), then the
amount of direct light reaching the top leaf surfaces of the
second/lower layer is the weighted average of the light attenuated by
all the parallel tree canopies in the canopy layer above, thus.
), then the
amount of direct light reaching the top leaf surfaces of the
second/lower layer is the weighted average of the light attenuated by
all the parallel tree canopies in the canopy layer above, thus.
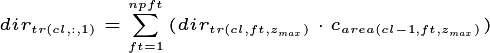
where  is the areal fraction of each canopy layer
occupied by each functional type and
is the areal fraction of each canopy layer
occupied by each functional type and  is the index of the
bottom canopy layer of each pft in each canopy layer (the subscripts
is the index of the
bottom canopy layer of each pft in each canopy layer (the subscripts
 and
and 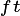 are implied but omitted from all
are implied but omitted from all
 references to avoid additional complications)
references to avoid additional complications)
Similarly, the sunlit fraction for a leaf layer ‘ ’ in the
second canopy layer (where
’ in the
second canopy layer (where  ) is
) is

where  is the weighted average sunlit fraction in the
bottom layer of a given canopy layer.
is the weighted average sunlit fraction in the
bottom layer of a given canopy layer.

Following through the sequence of equations for the simple single pft
and canopy layer approach above, the  and
and
 fluxes are also indexed by
fluxes are also indexed by  ,
,
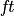 , and
, and  . The diffuse radiation reflectance ratio
. The diffuse radiation reflectance ratio
 is also calculated in a manner that homogenizes fluxes
between canopy layers. For the canopy layer nearest the soil
(
is also calculated in a manner that homogenizes fluxes
between canopy layers. For the canopy layer nearest the soil
( =
=  ). For the top canopy layer
(
). For the top canopy layer
( =1), a weighted average reflectance from the lower layers
is used as the baseline, in lieu of the soil albedo. Thus:
=1), a weighted average reflectance from the lower layers
is used as the baseline, in lieu of the soil albedo. Thus:

For the iterative flux resolution, the upwards and downwards fluxes are
also averaged between canopy layers, thus where 
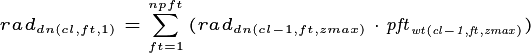
and where  =1, and
=1, and 

The remaining terms in the radiation calculations are all also indexed
by  ,
, 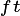 and
and  so that the fraction of
absorbed radiation outputs are termed
so that the fraction of
absorbed radiation outputs are termed 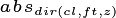 and
and
 . The sunlit and shaded absorption rates are
therefore
. The sunlit and shaded absorption rates are
therefore
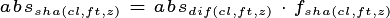
and

The albedo of the mixed pft canopy is calculated as the weighted average
of the upwards radiation from the top leaf layer of each pft where
 =1:
=1:

The radiation absorbed by the soil after passing through through under-storey vegetation is:

to which is added the diffuse flux coming directly from the upper canopy and hitting no understorey vegetation.

and the direct flux coming directly from the upper canopy and hitting no understorey vegetation.

These changes to the radiation code are designed to be structurally flexible, and the scheme may be collapsed down to only include on canopy layer, functional type and pft for testing if necessary.
Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Leaf angle distribution parameter |
none |
ft |
|
Fraction of light reflected by leaf surface |
none |
ft |
|
Fraction of light transmitted by leaf surface |
none |
ft |
|
Fraction of light reflected by soil |
none |
direct vs diffuse |
1.9. Photosynthesis¶
1.9.1. Fundamental photosynthetic physiology theory¶
In this section we describe the physiological basis of the
photosynthesis model before describing its application to the FATES
canopy structure. This description in this section is largely repeated
from the Oleson et al. CLM4.5 technical note but included here for
comparison with its implementation in FATES. Photosynthesis in C3
plants is based on the model of Farquhar 1980 as
modified by Collatz et al. (1991). Photosynthetic assimilation
in C4 plants is based on the model of Collatz et al. (1991).
In both models, leaf photosynthesis,  (
( mol CO
mol CO m
m s
s ) is
calculated as the minimum of three potentially limiting fluxes,
described below:
) is
calculated as the minimum of three potentially limiting fluxes,
described below:

The RuBP carboxylase (Rubisco) limited rate of carboxylation
 (
( mol CO
mol CO m
m s
s ) is determined as
) is determined as

where  is the internal leaf CO
is the internal leaf CO partial
pressure (Pa) and
partial
pressure (Pa) and  ) is the O
) is the O partial pressure (Pa).
partial pressure (Pa).  and
and 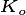 are the
Michaelis-Menten constants (Pa) for CO
are the
Michaelis-Menten constants (Pa) for CO and
O
and
O . These vary with vegetation temperature
. These vary with vegetation temperature 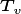 (
( C) according to an Arrhenious function described in
Oleson et al. 2013.
C) according to an Arrhenious function described in
Oleson et al. 2013.  is the leaf layer
photosynthetic capacity (
is the leaf layer
photosynthetic capacity ( mol CO
mol CO m
m s
s ).
).
The maximum rate of carboxylation allowed by the capacity to regenerate
RuBP (i.e., the light-limited rate)  (
( mol
CO
mol
CO m
m s
s ) is
) is

To find  , the electron transport rate (
, the electron transport rate ( mol
CO
mol
CO m
m s
s ), we solve the
following quadratic term and take its smaller root,
), we solve the
following quadratic term and take its smaller root,
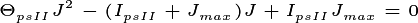
where  is the maximum potential rate of electron
transport (
is the maximum potential rate of electron
transport ( mol m
mol m s
s ),
),
 is the is the light utilized in electron transport by
photosystem II (
is the is the light utilized in electron transport by
photosystem II ( mol m
mol m s
s ) and
) and
 is is curvature parameter.
is is curvature parameter.  is
determined as
is
determined as

where  is the absorbed photosynthetically active radiation
(Wm:math:^{-2}) for either sunlit or shaded leaves (
is the absorbed photosynthetically active radiation
(Wm:math:^{-2}) for either sunlit or shaded leaves ( and
and  ).
).  is converted to photosynthetic
photon flux assuming 4.6
is converted to photosynthetic
photon flux assuming 4.6  mol photons per joule. Parameter
values are
mol photons per joule. Parameter
values are  = 0.7 for C3 and
= 0.7 for C3 and  =
0.85 for C4 plants.
=
0.85 for C4 plants.
The export limited rate of carboxylation for C3 plants and the PEP
carboxylase limited rate of carboxylation for C4 plants  (also in
(also in  mol CO
mol CO m
m s
s ) is
) is
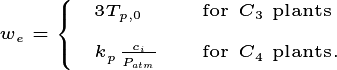
 is the triose-phosphate limited rate of photosynthesis,
which is equal to
is the triose-phosphate limited rate of photosynthesis,
which is equal to  .
.  is the initial
slope of C4 CO
is the initial
slope of C4 CO response curve. The Michaelis-Menten
constants
response curve. The Michaelis-Menten
constants  and
and  are modeled as follows,
are modeled as follows,
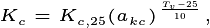

where  = 30.0 and
= 30.0 and  = 30000.0 are values
(Pa) at 25
= 30000.0 are values
(Pa) at 25  C, and
C, and  = 2.1 and
= 2.1 and  =1.2 are the relative changes in
=1.2 are the relative changes in  and
and  respectively, for a 10
respectively, for a 10 C change in temperature. The
CO
C change in temperature. The
CO compensation point
compensation point  (Pa) is
(Pa) is

where the term 0.21 represents the ratio of maximum rates of oxygenation to carboxylation, which is virtually constant with temperature Farquhar, 1980.
1.9.2. Resolution of the photosynthesis theory within the FATES canopy structure.¶
The photosynthesis scheme is modified from the CLM4.5 model to give
estimates of photosynthesis, respiration and stomatal conductance for a
three dimenstional matrix indexed by canopy level ( ), plant
functional type (
), plant
functional type (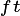 ) and leaf layer (
) and leaf layer ( ). We conduct the
photosynthesis calculations at each layer for both sunlit and shaded
leaves. Thus, the model also generates estimates of
). We conduct the
photosynthesis calculations at each layer for both sunlit and shaded
leaves. Thus, the model also generates estimates of  and
and  indexed in the same three dimensional matrix. In this
implementation, some properties (stomatal conductance parameters,
top-of-canopy photosynthetic capacity) vary with plant functional type,
and some vary with both functional type and canopy depth (absorbed
photosynthetically active radiation, nitrogen-based variation in
photosynthetic properties). The remaining drivers of photosynthesis
(
indexed in the same three dimensional matrix. In this
implementation, some properties (stomatal conductance parameters,
top-of-canopy photosynthetic capacity) vary with plant functional type,
and some vary with both functional type and canopy depth (absorbed
photosynthetically active radiation, nitrogen-based variation in
photosynthetic properties). The remaining drivers of photosynthesis
(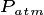 ,
,  ,
,  ,
,  , temperature,
atmospheric CO
, temperature,
atmospheric CO ) remain the same throughout the canopy. The
rate of gross photosynthesis (
) remain the same throughout the canopy. The
rate of gross photosynthesis ( )is the smoothed
minimum of the three potentially limiting processes (carboxylation,
electron transport, export limitation), but calculated independently for
each leaf layer:
)is the smoothed
minimum of the three potentially limiting processes (carboxylation,
electron transport, export limitation), but calculated independently for
each leaf layer:
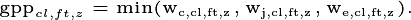
For  , we use
, we use

where  now varies with PFT, canopy depth and layer
(see below). Internal leaf
now varies with PFT, canopy depth and layer
(see below). Internal leaf  (
( is
tracked seperately for each leaf layer. For the light limited rate
is
tracked seperately for each leaf layer. For the light limited rate
 , we use
, we use
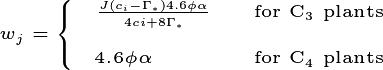
where  is calculated as above but based on the absorbed
photosynthetically active radiation(
is calculated as above but based on the absorbed
photosynthetically active radiation(  ) for either
sunlit or shaded leaves in Wm
) for either
sunlit or shaded leaves in Wm . Specifically,
. Specifically,
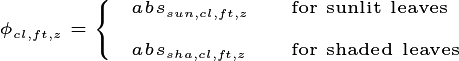
The export limited rate of carboxylation for C3 plants and the PEP
carboxylase limited rate of carboxylation for C4 plants  (also in
(also in  mol CO
mol CO m
m s
s ) is calculated in a similar fashion,
) is calculated in a similar fashion,

1.9.3. Variation in plant physiology with canopy depth¶
Both  and
and  vary with vertical depth in
the canopy on account of the well-documented reduction in canopy
nitrogen through the leaf profile, see Bonan et al. 2012 for
details). Thus, both
vary with vertical depth in
the canopy on account of the well-documented reduction in canopy
nitrogen through the leaf profile, see Bonan et al. 2012 for
details). Thus, both  and
and  are indexed
by by
are indexed
by by  ,
,  and
and  according to the nitrogen
decay coefficient
according to the nitrogen
decay coefficient  and the amount of vegetation area shading
each leaf layer
and the amount of vegetation area shading
each leaf layer  ,
,
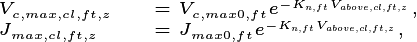
where  and
and  are the top-of-canopy
photosynthetic rates.
are the top-of-canopy
photosynthetic rates.  is the sum of exposed leaf area
index (
is the sum of exposed leaf area
index ( ) and the exposed stem area index
(
) and the exposed stem area index
( )( m
)( m m
m ).
Namely,
).
Namely,

The vegetation index shading a particular leaf layer in the top canopy layer is equal to

For lower canopy layers, the weighted average vegetation index of the
canopy layer above ( ) is added to this within-canopy
shading. Thus,
) is added to this within-canopy
shading. Thus,

where  is calculated as
is calculated as
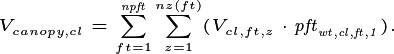
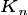 is the coefficient of nitrogen decay with canopy depth.
The value of this parameter is taken from the work of
Lloyd et al. 2010 who determined, from 204 vertical profiles
of leaf traits, that the decay rate of N through canopies of tropical
rainforests was a function of the
is the coefficient of nitrogen decay with canopy depth.
The value of this parameter is taken from the work of
Lloyd et al. 2010 who determined, from 204 vertical profiles
of leaf traits, that the decay rate of N through canopies of tropical
rainforests was a function of the  at the top of the
canopy. They obtain the following term to predict
at the top of the
canopy. They obtain the following term to predict 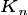 ,
,

where  is again in
is again in  mol CO
mol CO m
m s
s .
.
1.9.4. Water Stress on gas exchange¶
The top of canopy leaf photosynthetic capacity,  , is
also adjusted for the availability of water to plants as
, is
also adjusted for the availability of water to plants as
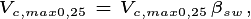
where the adjusting factor  ranges from one when the
soil is wet to zero when the soil is dry. It depends on the soil water
potential of each soil layer, the root distribution of the plant
functional type, and a plant-dependent response to soil water stress,
ranges from one when the
soil is wet to zero when the soil is dry. It depends on the soil water
potential of each soil layer, the root distribution of the plant
functional type, and a plant-dependent response to soil water stress,

where  is a plant wilting factor for layer
is a plant wilting factor for layer  and
and
 is the fraction of roots in layer
is the fraction of roots in layer  .The plant
wilting factor
.The plant
wilting factor  is
is

where  is the soil water matric potential (mm) and
is the soil water matric potential (mm) and
 and
and  are the soil water potential (mm)
when stomata are fully closed or fully open, respectively. The term in
brackets scales
are the soil water potential (mm)
when stomata are fully closed or fully open, respectively. The term in
brackets scales 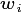 the ratio of the effective porosity (after
accounting for the ice fraction) relative to the total porosity.
the ratio of the effective porosity (after
accounting for the ice fraction) relative to the total porosity.
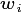 = 0 when the temperature of the soil layer (
= 0 when the temperature of the soil layer ( ) is below some threshold (-2:math:^{o}C) or when there is no liquid
water in the soil layer (
) is below some threshold (-2:math:^{o}C) or when there is no liquid
water in the soil layer ( ). For more details
on the calculation of soil matric potential, see the CLM4.5 technical
note.
). For more details
on the calculation of soil matric potential, see the CLM4.5 technical
note.
1.9.4.1. Variation of water stress and water uptake within tiles¶
The remaining drivers of the photosynthesis model remain constant
(atmospheric CO and O
and O and canopy temperature)
throughout the canopy, except for the water stress index
and canopy temperature)
throughout the canopy, except for the water stress index
 .
.  must be indexed by
must be indexed by 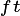 ,
because plants of differing functional types have the capacity to have
varying root depth, and thus access different soil moisture profile and
experience differing stress functions. Thus, the water stress function
applied to gas exchange calculation is now calculated as
,
because plants of differing functional types have the capacity to have
varying root depth, and thus access different soil moisture profile and
experience differing stress functions. Thus, the water stress function
applied to gas exchange calculation is now calculated as

where  is the water stress at each soil layer
is the water stress at each soil layer  and
and  is the root fraction of each PFT’s root mass in
layer
is the root fraction of each PFT’s root mass in
layer  . Note that this alteration of the
. Note that this alteration of the  parameter also necessitates recalculation of the vertical water
extraction profiles. In the original model, the fraction of extraction
from each layer (
parameter also necessitates recalculation of the vertical water
extraction profiles. In the original model, the fraction of extraction
from each layer ( ) is the product of a single root
distribution, because each patch only has one plant functional type. In
FATES, we need to calculate a new weighted patch effective rooting
depth profile
) is the product of a single root
distribution, because each patch only has one plant functional type. In
FATES, we need to calculate a new weighted patch effective rooting
depth profile  as the weighted average of the
functional-type level stress functions and their relative contributions
to canopy conductance. Thus for each layer
as the weighted average of the
functional-type level stress functions and their relative contributions
to canopy conductance. Thus for each layer  , the extraction
fraction is summed over all PFTs as
, the extraction
fraction is summed over all PFTs as

where  is the number of soil layers,
is the number of soil layers,  is
the total canopy (see section 9 for details) and
is
the total canopy (see section 9 for details) and  is the
canopy conductance for plant functional type
is the
canopy conductance for plant functional type 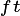 ,
,

1.9.5. Aggregation of assimilated carbon into cohorts¶
The derivation of photosynthetic rates per leaf layer, as above, give us
the estimated rate of assimilation for a unit area of leaf at a given
point in the canopy in  mol CO
mol CO m
m s
s . To allow the integration of these rates into fluxes
per individual tree, or cohort of trees (gCO:math:_2
tree
. To allow the integration of these rates into fluxes
per individual tree, or cohort of trees (gCO:math:_2
tree s
s ), they must be multiplied by the
amount of leaf area placed in each layer by each cohort. Each cohort is
described by a single functional type,
), they must be multiplied by the
amount of leaf area placed in each layer by each cohort. Each cohort is
described by a single functional type, 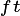 and canopy layer
and canopy layer
 flag, so the problem is constrained to integrating these
fluxes through the vertical profile (
flag, so the problem is constrained to integrating these
fluxes through the vertical profile ( ).
).
We fist make a weighted average of photosynthesis rates from sun
( ,
,  mol CO
mol CO m
m s
s ) and shade leaves (
) and shade leaves (
 ,
,  mol CO
mol CO m
m s
s ) as
) as
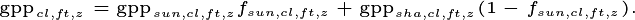
The assimilation per leaf layer is then accumulated across all the leaf
layers in a given cohort (coh) to give the cohort-specific gross
primary productivity ( ),
),

The  is the exposed leaf area which is
present in each leaf layer in m
is the exposed leaf area which is
present in each leaf layer in m m
m . (For all
the leaf layers that are completely occupied by a cohort, this is the
same as the leaf fraction of
. (For all
the leaf layers that are completely occupied by a cohort, this is the
same as the leaf fraction of  ). The fluxes are
converted from
). The fluxes are
converted from  mol into mol and then multiplied by 12 (the
molecular weight of carbon) to give units for GPP
mol into mol and then multiplied by 12 (the
molecular weight of carbon) to give units for GPP of KgC
cohort
of KgC
cohort s
s . These are integrated for each
timestep to give KgC cohort
. These are integrated for each
timestep to give KgC cohort day
day
Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Maximum carboxylation capacity |
|
ft |
|
Base Rate of Respiration |
gC
gN |
|
|
Temp. Response of stem and root respiration |
||
|
CN ratio of leaf matter |
gC/gN |
ft |
|
CN ratio of root matter |
gC/gN |
ft |
|
Growth Respiration Fraction |
none |
|
|
Water content when stomata close |
Pa |
ft |
|
Water content above which stomata are open |
Pa |
ft |
1.10. Plant respiration¶
Plant respiration per individual  (KgC individual
(KgC individual
 s
s ) is the sum of two terms, growth and
maintenance respiration
) is the sum of two terms, growth and
maintenance respiration  and
and 

Maintenance respiration is the sum of the respiration terms from four
different plant tissues, leaf,  , fine root
, fine root
 , coarse root
, coarse root  and stem
and stem
 , all also in (KgC individual
, all also in (KgC individual  s
s ) .
) .

1.10.1. Leaf maintenance respiration - Atkin et al. 2017¶
The Atkin et al. 2017 leaf maintenance respiration (Rdark) model includes temperature acclimation. We first determine the top-of-canopy Rdark rate.
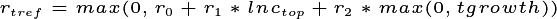
where  is the PFT-dependent base Rdark rate,
is the PFT-dependent base Rdark rate,
 is a parameter that determines the effects of nitrogen availability
on Rdark,
is a parameter that determines the effects of nitrogen availability
on Rdark,  is a parameter that determines the effects of temperature
on Rdark, and
is a parameter that determines the effects of temperature
on Rdark, and  is the lagged vegetation temperature averaged over
the acclimation timescale. We use
is the lagged vegetation temperature averaged over
the acclimation timescale. We use  = 0.2061 and
= 0.2061 and  = -0.0402
following Atkin et al. 2017.
= -0.0402
following Atkin et al. 2017.
At very high temperatures, and with low values of
 , the whole term can become negative, and we therefore cap it at 0 to prevent negative Rdark.
, the whole term can become negative, and we therefore cap it at 0 to prevent negative Rdark.
We scale vertically through the canopy based on nitrogen availability following
Lloyd et al. 2010, in the same way that  values are scaled uisng
values are scaled uisng  , described above.
, described above.

where

and

where  is PFT-dependent maximum carboxylation rate of rubisco at the top
of the canopy at 25 degrees C, and
is PFT-dependent maximum carboxylation rate of rubisco at the top
of the canopy at 25 degrees C, and  is the cumulative LAI, top down,
to the leaf layer of interest.
is the cumulative LAI, top down,
to the leaf layer of interest.
We then adjust Rdark for current vegetation temperature ( ).
).

where  is the reference temperature of 25 degrees C, and
is the reference temperature of 25 degrees C, and  and
and  are parameters from Heskel et al. 2016, set as
are parameters from Heskel et al. 2016, set as
 = 0.1012 and
= 0.1012 and  = -0.0005.
= -0.0005.
1.10.2. Leaf maintenance respiration - Ryan 1991¶
To calculate canopy leaf respiration following Ryan et al. 1991,
we first determine the top-of-canopy leaf respiration rate
( , gC s
, gC s m
m ) is
calculated from a base rate of respiration per unit leaf nitrogen
derived from Ryan et al. 1991. The base rate for leaf
respiration (
) is
calculated from a base rate of respiration per unit leaf nitrogen
derived from Ryan et al. 1991. The base rate for leaf
respiration (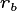 ) is 2.525 gC/gN s
) is 2.525 gC/gN s ,
,

where 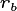 is the base rate of metabolism (2.525 x
10
is the base rate of metabolism (2.525 x
10 gC/gN s
gC/gN s . This base rate is adjusted
assuming a Q
. This base rate is adjusted
assuming a Q of 1.5 to scale from the baseline of 20C to
the CLM default base rate temperature of 25C. For use in the
calculations of net photosynthesis and stomatal conductance, leaf
respiration is converted from gC s
of 1.5 to scale from the baseline of 20C to
the CLM default base rate temperature of 25C. For use in the
calculations of net photosynthesis and stomatal conductance, leaf
respiration is converted from gC s m
m , into
, into
 mol CO
mol CO m
m s
s (
( ).
).
This top-of-canopy flux is scaled to account for variation in
 through the vertical canopy, in the same manner as the
through the vertical canopy, in the same manner as the
 values are scaled using
values are scaled using  .
.

Leaf respiration is also adjusted such that it is reduced by drought
stress,  , and canopy temperature,
, and canopy temperature,  .
For details of the temperature functions affecting leaf respiration see
the CLM4 technical note, Section 8, Equations 8.13 and 8.14. The
adjusted leaf level fluxes are scaled to individual-level (gC individual
.
For details of the temperature functions affecting leaf respiration see
the CLM4 technical note, Section 8, Equations 8.13 and 8.14. The
adjusted leaf level fluxes are scaled to individual-level (gC individual
 s
s ) in the same fashion as the
) in the same fashion as the
 calculations
calculations

The stem and the coarse-root respiration terms are derived using the same base rate of respiration per unit of tissue Nitrogen.

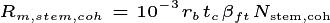
Here,  is a temperature relationship based on a
is a temperature relationship based on a
 value of 1.5, where
value of 1.5, where  is the vegetation
temperature. We use a base rate of 20 here as, again, this is the
baseline temperature used by Ryan et al. 1991. The
10
is the vegetation
temperature. We use a base rate of 20 here as, again, this is the
baseline temperature used by Ryan et al. 1991. The
10 converts from gC invididual
converts from gC invididual s
s to KgC invididual
to KgC invididual s
s

The tissue N contents for live sapwood are derived from the leaf CN ratios, and for fine roots from the root CN ratio as:

and

where  and
and  are
the biomass pools of sapwood and live root biomass respectively (KgC
individual) and
are
the biomass pools of sapwood and live root biomass respectively (KgC
individual) and  is the fraction of coarse root
tissue in the root pool (0.5 for woody plants, 0.0 for grasses and
crops). We assume here that stem CN ratio is the same as the leaf C:N
ratio, for simplicity. The final maintenance respiration term is derived
from the fine root respiration, which accounts for gradients of
temperature in the soil profile and thus calculated for each soil layer
is the fraction of coarse root
tissue in the root pool (0.5 for woody plants, 0.0 for grasses and
crops). We assume here that stem CN ratio is the same as the leaf C:N
ratio, for simplicity. The final maintenance respiration term is derived
from the fine root respiration, which accounts for gradients of
temperature in the soil profile and thus calculated for each soil layer
 as follows:
as follows:

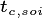 is a function of soil temperature in layer
is a function of soil temperature in layer  that has the same form as that for stem respiration, but uses vertically
resolved soil temperature instead of canopy temperature. In the CLM4.5,
only coarse and not fine root respriation varies as a function of soil
depth, and we maintain this assumption here, although it may be altered
in later versions.
that has the same form as that for stem respiration, but uses vertically
resolved soil temperature instead of canopy temperature. In the CLM4.5,
only coarse and not fine root respriation varies as a function of soil
depth, and we maintain this assumption here, although it may be altered
in later versions.
The source of maintenance respiration is the plant’s carbon storage
pool, which is updated daily. For plants that are in long-term
negative carbon balance, FATES assumes a tradoff between reduced
maintenance respiration expenditures and increased carbon-starvation
mortality (see section ‘Plant Mortality’). This reduction of
maintenance respiration during carbon starvation is consistent with
observations of trees under acute carbon stress (Sevanto et al.,
2014). Because the physiologic basis and form of this process is
poorly constrained, we use heuristic functions here to define these
processes. First, we define a target carbon storage pool ( ):
):

where  is a pft-specific parameter that linearly relates the target
storage pool to the target leaf biomass
is a pft-specific parameter that linearly relates the target
storage pool to the target leaf biomass  . If a given plant
is unable to achieve its target carbon storage because of having a
negative NPP at any given time, then its actual storage pool
. If a given plant
is unable to achieve its target carbon storage because of having a
negative NPP at any given time, then its actual storage pool
 will drop below the target storage pool
will drop below the target storage pool  . Then FATES
sets the fractional rate of maintenance respiration (R) on the ratio of
. Then FATES
sets the fractional rate of maintenance respiration (R) on the ratio of  to
to  :
:

where  is a parameter that governs the curvature of the
respiration reduction function. This parameter is specific to a given
PFT.
is a parameter that governs the curvature of the
respiration reduction function. This parameter is specific to a given
PFT.
The growth respiration,  is a fixed
fraction
is a fixed
fraction  of the carbon remaining after maintenance
respiration has occurred.
of the carbon remaining after maintenance
respiration has occurred.

Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Rate of reduction of N through the canopy |
none |
|
|
Base Rate of Respiration |
gC
gN |
|
|
Temp. Response of stem and root respiration |
||
|
CN ratio of leaf matter |
gC/gN |
ft |
|
CN ratio of root matter |
gC/gN |
ft |
|
Growth Respiration Fraction |
none |
ft |
|
Low-Storage Maintenance Respiration Reduction Param. |
none |
ft |
1.11. Stomatal Conductance¶
1.11.1. Fundamental stomatal conductance theory¶
Within FATES, leaf-level stomatal conductance is representated by two main
approaches. The first calculates stomatal conductance
(1/resistance) using the Ball-Berry model as implemented in
CLM4.5 (http://www.cesm.ucar.edu/models/cesm1.2/clm/CLM45_Tech_Note.pdf) and
described by Collatz et al. (1991) and
Sellers et al. 1996. The model relates stomatal conductance
(i.e., the inverse of resistance) to net leaf photosynthesis, scaled by the
relative humidity at the leaf surfaceand the CO concentration at the
leaf surface. The primary difference between the CLM implementation and that used by
Collatz et al. (1991) and Sellers et al. (1996) is
that they used net photosynthesis (i.e., leaf photosynthesis minus leaf
respiration) instead of gross photosynthesis. As implemented here,
stomatal conductance equals the minimum conductance (
concentration at the
leaf surface. The primary difference between the CLM implementation and that used by
Collatz et al. (1991) and Sellers et al. (1996) is
that they used net photosynthesis (i.e., leaf photosynthesis minus leaf
respiration) instead of gross photosynthesis. As implemented here,
stomatal conductance equals the minimum conductance ( ) when
gross photosynthesis (
) when
gross photosynthesis ( ) is zero. Leaf stomatal conductance is
) is zero. Leaf stomatal conductance is

where  is leaf stomatal resistance (s m
is leaf stomatal resistance (s m leaf area
leaf area
 mol
mol  ),
),  in units of
in units of
 mol
mol  m
m leaf area s
leaf area s is a plant functional
type dependent parameter equivalent to
is a plant functional
type dependent parameter equivalent to  in the Ball-Berry
model literature. This parameter is also scaled by the water stress
index
in the Ball-Berry
model literature. This parameter is also scaled by the water stress
index  . Similarly,
. Similarly,  is the slope of the
relationship (i.e. stomatal slope, or the
is the slope of the
relationship (i.e. stomatal slope, or the  term in the stomatal literature)
between stomatal conductance and the stomatal index, comprised of the leaf assimilation
rate,
term in the stomatal literature)
between stomatal conductance and the stomatal index, comprised of the leaf assimilation
rate,  (
( mol CO
mol CO m
m leaf area s
leaf area s ),
),
 is the CO
is the CO partial pressure at
the leaf surface (Pa),
partial pressure at
the leaf surface (Pa),  is the vapor pressure at the leaf
surface (Pa),
is the vapor pressure at the leaf
surface (Pa),  is the saturation vapor pressure (Pa) inside
the leaf at the vegetation temperature
is the saturation vapor pressure (Pa) inside
the leaf at the vegetation temperature  (K), and
(K), and  is the conductace (
is the conductace ( mol
mol m
m leaf area s
leaf area s )
when
)
when  = 0.
= 0.
The second (default) representation of stomatal conductance in FATES follows the Unified Stomatal Optimization (USO) theory, otherwise known as the Medlyn model of stomatal conductance (Medlyn et al. 2011). The Medlyn model calculates stomatal conductance (i.e., the inverse of resistance) based on net leaf photosynthesis, the vapor pressure deficit, and the CO2 concentration at the leaf surface. Leaf stomatal resistance is calculated as:

Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Leaf stomatal resistance |
s m |
|
|
Leaf stomatal conductance |
|
|
|
Minimum stomatal conductance or the cuticular conductance |
|
ft |
|
Soil water stress factor |
none |
|
|
Vapor pressure deficit at the leaf surface |
kPa |
|
|
Stomatal slope |
kPa |
ft |
|
Leaf net photosynthesis |
|
|
|
|
Pa |
|
|
Atmospheric pressure |
Pa |
In both models leaf resistance is converted from units of s m mol
mol to s m
to s m as: 1 s m
as: 1 s m =
=
 R
R (
( mol
mol m
m s), where
R
s), where
R is the universal gas constant (J K
is the universal gas constant (J K kmol
kmol ) and
) and  is the atmospheric
potential temperature (K).
is the atmospheric
potential temperature (K).
Both  and
and  are PFT-specific parameters. The default
values for the Ball-Berry and Medlyn stomatal conductance model representations
are provide below:
are PFT-specific parameters. The default
values for the Ball-Berry and Medlyn stomatal conductance model representations
are provide below:
PFT Name |
Ball-Berry |
Medlyn |
|---|---|---|
Broadleaf evergreen tropical tree |
8 |
4.1 |
Needleleaf evergreen extratropical tree |
8 |
2.3 |
Needleleaf colddecid extratropical tree |
8 |
2.3 |
Broadleaf evergreen extratropical tree |
8 |
4.1 |
Broadleaf hydrodecid tropical tree |
8 |
4.4 |
Broadleaf colddecid extratropical tree |
8 |
4.4 |
Broadleaf evergreen extratropical shrub |
8 |
4.7 |
Broadleaf hydrodecid extratropical shrub |
8 |
4.7 |
Broadleaf colddecid extratropical shrub |
8 |
4.7 |
Arctic |
8 |
2.2 |
Cool |
8 |
5.3 |
|
8 |
1.6 |
For both the Ball-Berry and Medlyn stomatal models the default  is
1000 for all PFTs.
is
1000 for all PFTs.
1.11.2. Numerical implementation of the Medlyn stomatal conductance model¶
Photosynthesis is calculated assuming there is negligible capacity to store  and water vapor at the leaf surface so that:
and water vapor at the leaf surface so that:

The terms 1.4 and 1.6 are the ratios of diffusivity of  to
to  for the leaf
boundary layer resistance and stomatal resistance. The transpiration fluxes are related as:
for the leaf
boundary layer resistance and stomatal resistance. The transpiration fluxes are related as:


Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Atmospheric |
Pa |
|
|
Internal leaf |
Pa |
|
|
Leaf boundary layer resistance |
s m |
|
|
Vapor pressure of air |
Pa |
|
|
Saturation vapor pressure |
Pa |
|
|
Vapor pressure at the leaf surface |
Pa |
|
|
Specific humidity of canopy air |
kg kg
|
In the Medlyn model, an initial guess of  is obtained assuming the ratio between
is obtained assuming the ratio between
 and
and  (0.7 for
(0.7 for  plants and 0.4 for
plants and 0.4 for  plants)
to calculate
plants)
to calculate  based on Farquhar 1980. Solving for
based on Farquhar 1980. Solving for  :
:

 can be represented as:
can be represented as:

Where  is a function of temperature
is a function of temperature
Substitution of  following
following  gives an expression for stomatal resistance
(
gives an expression for stomatal resistance
( ) as a function of photosynthesis (
) as a function of photosynthesis ( ), given here in terms of conductance with
), given here in terms of conductance with 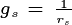 and
and 

where
![b = -[2(b_{ft} \times \beta_{sw}+d)+\frac{(m_{ft})^{2}d^{2}}{g_{b}D_{a}}]](_images/math/23fb19d4103f0375489894b0308cbebbc4eb05db.png)
![c = (b_{ft} \times \beta_{sw})^{2}+[2g_{0} \times \beta_{sw}+d(1-\frac{{m_{ft}}^{2}}{D_{a}})]d](_images/math/f8de93f27786fffce52f6dc2a59b92a3833582ce.png)
and
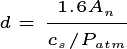

Stomatal conductance is the larger of the two roots that satisfies the quadratic equation.
Values for  are given by:
are given by:

The equations for  , and
, and  are solved iteratively until
are solved iteratively until  converges.
Iteration will be exited if convergence criteria is met or if at least five iterations are completed.
converges.
Iteration will be exited if convergence criteria is met or if at least five iterations are completed.
1.11.3. Resolution of stomatal conductance theory in the FATES canopy structure¶
The stomatal conductance is calculated, as with photosynthesis, for each
canopy, PFT and leaf layer. The HLM code requires a single canopy
conductance estimate to be generated from the multi-layer multi-PFT
array. In previous iterations of the HLM, sun and shade-leaf specific
values have been reported and then averaged by their respective leaf
areas. In this version, the total canopy condutance
 , is calculated as the sum of the cohort-level
conductance values.
, is calculated as the sum of the cohort-level
conductance values.
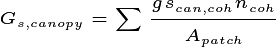
Cohort conductance is the sum of the inverse of the leaf resistances at
each canopy layer ( ) multipled by the area of each
cohort.
) multipled by the area of each
cohort.
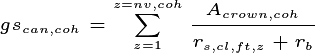
1.12. Control of Leaf Area Index¶
The leaf area  (m
(m ) of each cohort is
calculated from leaf biomass
) of each cohort is
calculated from leaf biomass  (kgC
individual
(kgC
individual ) and specific leaf area (SLA, m
) and specific leaf area (SLA, m kg
C
kg
C ). Leaf biomass
). Leaf biomass  is controlled by the
processes of phenology, allocation and turnover, described in detail in the
PARTEH submodule.
is controlled by the
processes of phenology, allocation and turnover, described in detail in the
PARTEH submodule.

However, using this model, where leaf area and crown area are both
functions of diameter, the leaf area index of each tree in a closed
canopy forest is always the same (where  =
=
 , irrespective of the growth conditions. To allow
greater plasticity in tree canopy structure, and for tree leaf area
index to adapt to prevailing conditions, we implemented a methodology
for removing those leaves in the canopy that exist in negative carbon
balance. That is, their total annual assimilation rate is insufficient
to pay for the turnover and maintenance costs associated with their
supportive root and stem tissue, plus the costs of growing the leaf. The
tissue turnover maintenance cost (KgC m
, irrespective of the growth conditions. To allow
greater plasticity in tree canopy structure, and for tree leaf area
index to adapt to prevailing conditions, we implemented a methodology
for removing those leaves in the canopy that exist in negative carbon
balance. That is, their total annual assimilation rate is insufficient
to pay for the turnover and maintenance costs associated with their
supportive root and stem tissue, plus the costs of growing the leaf. The
tissue turnover maintenance cost (KgC m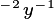 of leaf is
the total maintenance demand divided by the leaf area:
of leaf is
the total maintenance demand divided by the leaf area:

The net uptake for each leaf layer  in (KgC
m
in (KgC
m year
year ) is
) is

where  is the GPP of each layer of leaves in each tree (KgC
m
is the GPP of each layer of leaves in each tree (KgC
m year
year ),
),  is the rate
of leaf dark respiration (also KgC m
is the rate
of leaf dark respiration (also KgC m year
year ). We use an iterative scheme to define the cohort
specific canopy trimming fraction
). We use an iterative scheme to define the cohort
specific canopy trimming fraction  , on an annual
time-step, where
, on an annual
time-step, where

If the annual maintenance cost of the bottom layer of leaves (KgC m-2
year-1) is less than then the canopy is trimmed by an increment  (0.01), which is applied until the end of next calander year. Because this is an optimality model, there is an
issue of the timescale over which net assimilation is evaluated, the
timescale of response, and the plasticity of plants to respond to these
pressures. These properties should be investigated further in future
efforts.
(0.01), which is applied until the end of next calander year. Because this is an optimality model, there is an
issue of the timescale over which net assimilation is evaluated, the
timescale of response, and the plasticity of plants to respond to these
pressures. These properties should be investigated further in future
efforts.

We impose an arbitrary minimum value on the scope of canopy trimming of
 (0.5). If plants are able simply to drop all of
their canopy in times of stress, with no consequences, then tree
mortality from carbon starvation is much less likely to occur because of
the greatly reduced maintenance and turnover requirements.
(0.5). If plants are able simply to drop all of
their canopy in times of stress, with no consequences, then tree
mortality from carbon starvation is much less likely to occur because of
the greatly reduced maintenance and turnover requirements.
Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Fraction by which leaf mass is reduced next year |
none |
|
|
Minimum fraction to which leaf mass can be reduced |
none |
1.13. Phenology¶
In deciduous plant functional types, the target leaf biomass
( ) can be regulated through
the leaf elongation factor (
) can be regulated through
the leaf elongation factor ( ), a
non-dimensional, fractional quantity (i.e.,
), a
non-dimensional, fractional quantity (i.e.,  )
that quantifies the degree of environmental stress (cold or drought) experienced by the PFT
environmental conditions (temperature or moisture):
)
that quantifies the degree of environmental stress (cold or drought) experienced by the PFT
environmental conditions (temperature or moisture):

where (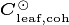 ) is the leaf biomass given size
and PFT when the cohort does not experience any stress. Importantly,
) is the leaf biomass given size
and PFT when the cohort does not experience any stress. Importantly,
 is not the absolute maximum leaf biomass given size, as
it can be still impacted by crown damage or canopy trimming.
is not the absolute maximum leaf biomass given size, as
it can be still impacted by crown damage or canopy trimming.
Two categories of deciduous PFTs are currently implemented in FATES, cold deciduous (summergreen) and
drought deciduous (raingreen). Cold deciduous plants are always hard-deciduous, meaning
that  can only be either 0 (leaves completely abscised) or
1 (PFTs will fully flush leaves provided that enough carbon storage is available). For drought-deciduous
PFTs, two strategies are available, hard-deciduous phenology, akin to the cold deciduous, and
the semi-deciduous phenology, where
can only be either 0 (leaves completely abscised) or
1 (PFTs will fully flush leaves provided that enough carbon storage is available). For drought-deciduous
PFTs, two strategies are available, hard-deciduous phenology, akin to the cold deciduous, and
the semi-deciduous phenology, where  can be any fraction between
0 and 1 (inclusive), which allows plants to partially abscise or partially flush leaves when drought
conditions are moderate. For evergreen PFTs,
can be any fraction between
0 and 1 (inclusive), which allows plants to partially abscise or partially flush leaves when drought
conditions are moderate. For evergreen PFTs, 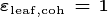 at all times.
at all times.
In addition to leaf phenology, in FATES it is possible to simulate active flushing and abscission of fine roots and stems in response to environmental conditions. In the case of fine roots, the main purpose is to reduce the maintenance of high-turnover tissues when plants are not assimilating carbon. In the case of stems, phenology is intended to be used for grass PFTs only, with the goal of avoiding numerical instabilities when running plant hydraulics (FATES-Hydro).
Fine-root and stem phenologies are controlled by PFT-specific drop fraction
parameters, namely  (FATES parameter
(FATES parameter fates_phen_fnrt_drop_fraction)
and  (FATES parameter
(FATES parameter fates_phen_stem_drop_fraction). Both
parameters range from 0 (perennial) to 1 (tissue phenology tracks leaf phenology), and are
used to determine elongation-factor-equivalent values for these tissues after the elongation
factor for leaves is determined:

In the next sections, we describe how  is
defined for non-evergreen PFTs.
is
defined for non-evergreen PFTs.
1.13.1. Cold Deciduous Leaf Phenology¶
1.13.1.1. Cold Leaf-out timing¶
The phenology model of Botta et al. 2000 is used in
FATES to determine the leaf-on timing. The Botta et al. model was
verified against satellite data and is one of the only globally verified
and published models of leaf-out phenology. This model differs from the
phenology model in the CLM4.5. The model simulates leaf-on date as a
function of the number of growing degree days (GDD), defined by the sum
of mean daily temperatures (
 ) above a
given threshold
) above a
given threshold  (
( ).
).

Budburst occurs when  exceeds a threshold
(
exceeds a threshold
( ). The threshold is modulated by the number of
chilling days experienced (
). The threshold is modulated by the number of
chilling days experienced ( ) where the mean daily temperature falls
below a threshold determined by Botta et al. 2000 as
) where the mean daily temperature falls
below a threshold determined by Botta et al. 2000 as  .
A greater number of chilling days means that fewer growing degree days are required before budburst:
.
A greater number of chilling days means that fewer growing degree days are required before budburst:
where  ,
,  and
and  (Botta et al. 2000).
In the Northern Hemisphere, counting of degree days begins on 1st January, and of
chilling days on 1st November. In the Southern Hemisphere, we use 1st July (growing degree days)
and 1st May (chilling days) instead.
(Botta et al. 2000).
In the Northern Hemisphere, counting of degree days begins on 1st January, and of
chilling days on 1st November. In the Southern Hemisphere, we use 1st July (growing degree days)
and 1st May (chilling days) instead.
If the growing degree days exceed the critical threshold, leaf-on is triggered by a change in the leaf elongation factor:

1.13.1.2. Cold Leaf-off timing¶
The leaf-off model is taken from the Sheffield Dynamic Vegetation Model
(SDGVM) and is similar to that for LPJ
Sitch et al. 2003 and IBIS
Foley et al. 1996 models. The average daily
temperatures of the previous 10 day period are stored. Senescence is
triggered when the number of days with an average temperature below  (
( ) rises above a threshold values
) rises above a threshold values
 , set at 5 days.
, set at 5 days.

1.13.1.3. Global implementation modifications¶
Because of the global implementation of the cold-deciduous phenology scheme, adjustments must be made to account for the possibility of cold-deciduous plants experiencing situations where no chilling period triggering leaf-off ever happens. If left unaccounted for, these leaves will last indefinitely, resulting in highly unrealistic behaviour. Therefore, we implement two additional rules. Firstly, if the number of days since the last senescence event was triggered is larger than 364, then leaf-off is triggered on that day. Secondly, if no chilling days have occured during the winter accumulation period, then leaf-on is not triggered. This means that in effect, where there are no cold periods, leaves will fall off and not come back on, meaning that cold-deciduous plants can only grow in places where there is a cold season.
Further to this rule, we introduce a ‘buffer’ time periods after leaf-on of 30 days, so that cold-snap periods in the spring cannot trigger a leaf senescence. The 30 day limit is an arbitrary limit. In addition, we constrain growing degree day accumulation to the second half of the year (July-December in the Northern hemisphere, or January-June in the Southern Hemisphere) and only allow GDD accumulation while the leaves are off.
1.13.2. Drought-deciduous leaf phenology (hard-deciduous)¶
The hard-, drought-deciduous phenology in FATES is based on CLM-4
(Dahlin et al. 2015; Oleson et al. 2013).
Both leaf flushing (growth) and leaf abscission (senescence) are controlled by
the plant available water (
 ),
a PFT-specific variable that is defined as the 10-day running average of the
soil matric potential across the rooting zone:
),
a PFT-specific variable that is defined as the 10-day running average of the
soil matric potential across the rooting zone:
![\psi_\mathrm{PFT,grid}\left(t\right) = \frac{1}{10} \,
\left[ \sum_{t'=t-9}^{t} \left( \frac{\displaystyle \sum_{k=k_\mathrm{root,PFT}}^{N_\mathrm{soil}-1} \psi\left(z_k,t'\right) \, r_{z_k,\mathrm{PFT}}}
{\displaystyle \sum_{k=k_\mathrm{root,PFT}}^{N_\mathrm{soil}-1} r_{z_k,\mathrm{PFT}}} \right) \right],](_images/math/18eca994a2803843047f2fcdb9ff64d95569f493.png)
where  is the soil matric potential of
layer
is the soil matric potential of
layer  at time
at time  ,
,  is the deepest
soil layer in the PFT’s rooting zone,
is the deepest
soil layer in the PFT’s rooting zone,  is the
fraction of roots of each plant functional type at each soil layer,
and
is the
fraction of roots of each plant functional type at each soil layer,
and  is the total number of soil layers. To avoid a
strong influence of the typically very thin top soil layer, we exclude this
layer when estimating
is the total number of soil layers. To avoid a
strong influence of the typically very thin top soil layer, we exclude this
layer when estimating  .
.
For the most part, drought conditions are based on a comparison
between 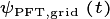 and a PFT-specific,
threshold parameter
and a PFT-specific,
threshold parameter ![\psi_\mathrm{PFT,drought} | \psi_\mathrm{PFT,drought} \in \left] -\infty,0\right[](_images/math/04d374facb988d4dec2324bfa2e8961d4ec6afa8.png) (
( ).
When
).
When  , we assume
drought conditions (plants likely to be or become leafless), and
when
, we assume
drought conditions (plants likely to be or become leafless), and
when  , we
assume non-drought conditions (plants likely to be or become fully flushed).
, we
assume non-drought conditions (plants likely to be or become fully flushed).
Similarly to the cold-deciduous phenology, we must include additional
constrains to ensure that plants are truly deciduous, even when the seasonal
cycle of 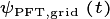 never crosses the drought
threshold. To prevent plants to remain leafless for long periods of
time, PFTs will forcibly flush leaves when the time since last flushing
(
never crosses the drought
threshold. To prevent plants to remain leafless for long periods of
time, PFTs will forcibly flush leaves when the time since last flushing
( ,
,  ) exceeds 395 days
(13 months). Likewise, the maximum time leaves can remain fully flushed is
defined by the PFT-specific leaf life span (
) exceeds 395 days
(13 months). Likewise, the maximum time leaves can remain fully flushed is
defined by the PFT-specific leaf life span ( ) or 12 months,
whichever is the shortest.
) or 12 months,
whichever is the shortest.
The use of a single-parameter threshold to define drought conditions can potentially
lead to a flickering behaviour, in which deciduous PFTs would flush and abscise leaves
multiple times if plant available water (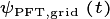 ) straddles
around
) straddles
around  . To prevent this, leaf abscission can only occur if
the time since last flushing has exceeded 90 days (3 months). Similarly, plants can only flush
leaves when the time since last abscission (
. To prevent this, leaf abscission can only occur if
the time since last flushing has exceeded 90 days (3 months). Similarly, plants can only flush
leaves when the time since last abscission ( ,
,  ) exceeds
a PFT-specific parameter (
) exceeds
a PFT-specific parameter ( ,
,  ). The only exception
to this rule is when a site is perennially moist, in which case PFTs can flush their leaves after
30 days, akin to a brevi-deciduous behaviour.
). The only exception
to this rule is when a site is perennially moist, in which case PFTs can flush their leaves after
30 days, akin to a brevi-deciduous behaviour.
The diagram below summarises how elongation factor is defined after accounting for the time-driven phenological cycles:
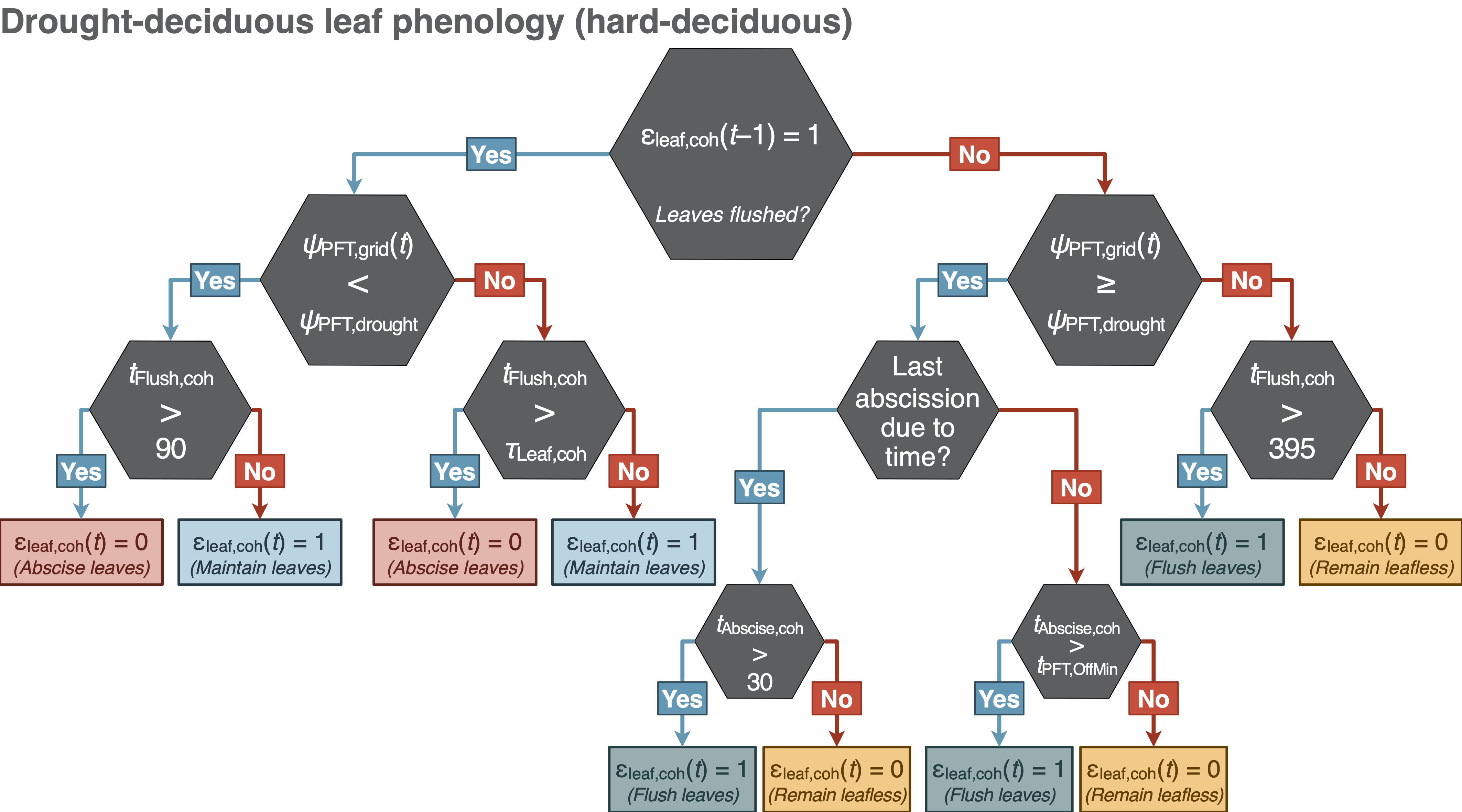
1.13.3. Drought-deciduous leaf phenology (semi-deciduous)¶
The semi-, drought-deciduous phenology in FATES is based on the hard-, drought-deciduous phenology, with a further modification in the elongation factor dynamics based on the ED-2.2 model (Longo et al. 2019). Semi-, drought-deciduous PFTs can partially abscise or partially flush leaves when drought conditions are moderate, and therefore can experience non-instantaneous flushing and abscission seasons.
To define the degree of abscission or flushing, we define a first guess for the elongation
factor ( ) that compares the plant available
water with two thresholds:
) that compares the plant available
water with two thresholds:
![\varepsilon^{\star}_\mathrm{leaf,PFT}(t) =
\max{\left[0,\min{\left(1,\frac{\psi_\mathrm{PFT,grid}\left(t\right)-\psi_\mathrm{PFT,drought}}{\psi_\mathrm{PFT,moist}-\psi_\mathrm{PFT,drought}}\right)}\right]}](_images/math/7c5e82c809db2bd6fcf0a85d9b0666c9401f7cbe.png)
where  (
(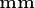 ) is a PFT-specific
parameter that defines the threshold above which plant available water is
no longer a limiting factor, and
) is a PFT-specific
parameter that defines the threshold above which plant available water is
no longer a limiting factor, and  defines
the threshold below which plant available water is strongly limiting. The latter
parameter is defined by the same parameter name in the FATES parameter file.
defines
the threshold below which plant available water is strongly limiting. The latter
parameter is defined by the same parameter name in the FATES parameter file.
Typically,  will be the actual elongation factor.
However, akin to the hard-deciduous PFTs, we must ensure that semi-deciduous PFTs still have
at least one abscission/flushing cycle every year, and that PFTs do not switch between abscising
and flushing phases too frequently, especially when the elongation factor is zero. To this end,
we define
will be the actual elongation factor.
However, akin to the hard-deciduous PFTs, we must ensure that semi-deciduous PFTs still have
at least one abscission/flushing cycle every year, and that PFTs do not switch between abscising
and flushing phases too frequently, especially when the elongation factor is zero. To this end,
we define  (
( ) to be the time since last full
abscission (i.e., when PFT lost all leaves), and
) to be the time since last full
abscission (i.e., when PFT lost all leaves), and  (
( )
as the time since last “out-of-leafless-state” flushing event. We then apply the set of rules
described in the figure below.
)
as the time since last “out-of-leafless-state” flushing event. We then apply the set of rules
described in the figure below.
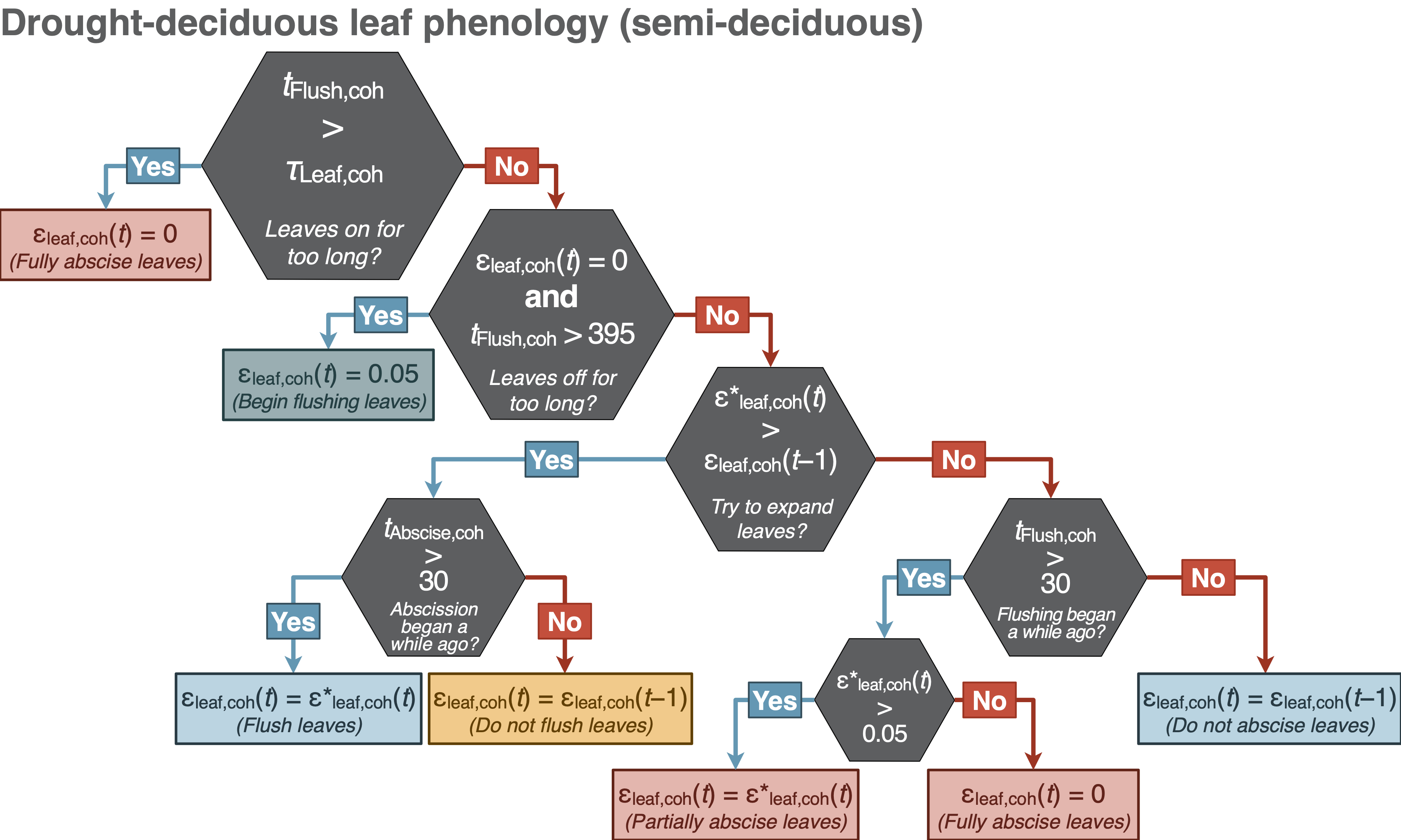
Note. The semi-deciduous implementation is still experimental, and may be revised as more experiments are carried out and more data become available.
1.13.4. Carbon allocation dynamics of deciduous plants¶
In the present version, phenology (i.e., the elongation factors) is updated at daily time steps. Once phenology is updated, carbon pools (i.e., plant tissues, storage and litter) are updated too.
To facilitate the tracking of phenology dynamics,
we define a flag variable ( ) that describes the
leaf phenology status of every cohort:
) that describes the
leaf phenology status of every cohort:

1.13.4.1. Expansion (flushing) phase¶
When cohorts are in expansion phase (i.e.,  ), carbon will
be transferred from the storage pool, based on the expected carbon stocks:
), carbon will
be transferred from the storage pool, based on the expected carbon stocks:

where  ,
,  and
and  are
respectively the maximum carbon biomass of leaves, fine roots and stems (sapwood + heartwood) that the cohort can attain given their size, PFT,
canopy trimming status, damage status and elongation factors.
are
respectively the maximum carbon biomass of leaves, fine roots and stems (sapwood + heartwood) that the cohort can attain given their size, PFT,
canopy trimming status, damage status and elongation factors.
In reality, the actual carbon stocks 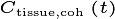 will depend on
both on
will depend on
both on  and the amount of carbon storage at the previous
time step (
and the amount of carbon storage at the previous
time step ( ), meaning
that
), meaning
that  . The transfer of
carbon from storage to the living tissues is solved by the Allocation and Reactive Transport (PARTEH) module.
. The transfer of
carbon from storage to the living tissues is solved by the Allocation and Reactive Transport (PARTEH) module.
1.13.4.2. Abscission phase¶
When cohorts are abscising tissues (i.e.,  ), the
updated carbon pools are defined based on the updated elongation factors:
), the
updated carbon pools are defined based on the updated elongation factors:
![\begin{array}{l}
C_\mathrm{leaf,coh}\left(t\right) = \min{\left[\varepsilon_\mathrm{leaf,coh}\left(t\right) \, C^{\odot}_\mathrm{leaf,coh}, C_\mathrm{leaf,coh}\left(t-1\right)\right]}, \\
C_\mathrm{root,coh}\left(t\right) = \min{\left[\varepsilon_\mathrm{root,coh}\left(t\right) \, C^{\odot}_\mathrm{root,coh}, C_\mathrm{root,coh}\left(t-1\right)\right]}, \\
C_\mathrm{stem,coh}\left(t\right) = \min{\left[\varepsilon_\mathrm{stem,coh}\left(t\right) \, C^{\odot}_\mathrm{stem,coh}, C_\mathrm{stem,coh}\left(t-1\right)\right]},
\end{array}](_images/math/cf79b54d51310940b56915be0b288f5931a48be9.png)
where 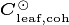 ,
,  and
and  are
respectively the maximum carbon biomass of leaves, fine roots and stems
(sapwood + heartwood) that the cohort can attain given their size, PFT,
canopy trimming status and damage status.
are
respectively the maximum carbon biomass of leaves, fine roots and stems
(sapwood + heartwood) that the cohort can attain given their size, PFT,
canopy trimming status and damage status.
Litter fluxes ( ) are defined as follows:
) are defined as follows:
![\begin{array}{l}
{\displaystyle l_\mathrm{leaf,coh}\left(t\right) = \frac{1}{\Delta t} \, \left[C_\mathrm{leaf,coh}\left(t-1\right) - C_\mathrm{leaf,coh}\left(t\right)\right]}, \\
{\displaystyle l_\mathrm{root,coh}\left(t\right) = \frac{1}{\Delta t} \, \left[C_\mathrm{root,coh}\left(t-1\right) - C_\mathrm{root,coh}\left(t\right)\right]}, \\
{\displaystyle l_\mathrm{stem,coh}\left(t\right) = \frac{1}{\Delta t} \, \left[C_\mathrm{stem,coh}\left(t-1\right) - C_\mathrm{stem,coh}\left(t\right)\right]}, \\
\end{array}](_images/math/8eefbe650cc62cda3f25e6cb796f79c8ae34dacd.png)
where 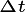 is the phenological time step.
is the phenological time step.
During abscission phase, cold-deciduous PFTs will use any storage carbon available to bring living tissues to the
expected level (i.e.,  ), similarly to what
occurs during the expansion (flushing) phase. This has minimum impact on cold-deciduous viability
because tissue turnover rate is a function of temperature, and therefore the costs are low during their
leaf-off season. This is not the case for drought deciduous, because the atmospheric
temperature (and the maintenance costs) are typically high in the leaf-off season, particularly in dry
tropical ecosystems. Therefore, when drought-deciduous PFTs status is
), similarly to what
occurs during the expansion (flushing) phase. This has minimum impact on cold-deciduous viability
because tissue turnover rate is a function of temperature, and therefore the costs are low during their
leaf-off season. This is not the case for drought deciduous, because the atmospheric
temperature (and the maintenance costs) are typically high in the leaf-off season, particularly in dry
tropical ecosystems. Therefore, when drought-deciduous PFTs status is  ,
they completely halt allocation to any tissue, and all carbon acquired during the abscission phase (only
possible when
,
they completely halt allocation to any tissue, and all carbon acquired during the abscission phase (only
possible when  ) is transferred to carbon storage.
) is transferred to carbon storage.
Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Threshold of cold days for senescence |
none |
|
|
Threshold for counting growing degree days |
|
|
|
Fraction of active abscission of fine roots, relative to leaves. |
none |
|
|
Fraction of active abscission of stems, relative to leaves. |
none |
|
|
Threshold below which drought deciduous cohorts abscise all leaves |
|
|
|
Threshold above which water is no longer a limiting factor |
|
|
|
Minimum leaf-off time for hard-, drought deciduous PFTs |
|
1.14. Seed Dynamics and Recruitment¶
The production of seeds and their subsequent germination is a process
that must be captured explicitly or implicitly in vegetation models. FATES contains a seed bank model designed to allow the dynamics of
seed production and germination to be simulated independently. In the
ED1.0 model, seed recruitment occurs in the same timestep as allocation
to seeds, which prohibits the survival of a viable seed bank through a
period of disturbance or low productivity (winter, drought). In FATES, a plant functional type specific seed bank is tracked in
each patch ( KgC m
KgC m ), whose rate of
change (KgC m
), whose rate of
change (KgC m y
y ) is the balance of inputs,
germination and decay:
) is the balance of inputs,
germination and decay:

where  ,
,  and
and 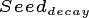 are the production, germination and decay (or onset of inviability) of
seeds, all in KgC m
are the production, germination and decay (or onset of inviability) of
seeds, all in KgC m year
year .
.
Seeds are assumed to be distributed evenly across the site (in this version of the model), so the total input to the seed pool is therefore the sum of all of the reproductive output of all the cohorts in each patch of the correct PFT type.

Seed decay is the sum of all the processes that reduce the number of
seeds, taken from Lischke et al. 2006. Firstly, the rate at
which seeds become inviable is described as a constant rate  (y:math:^{-1}) which is set to 0.51, the mean of the parameters used
by Lischke et al. 2006.
(y:math:^{-1}) which is set to 0.51, the mean of the parameters used
by Lischke et al. 2006.
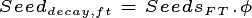
The seed germination flux is also prescribed as a fraction of the
existing pool ( ), but with a cap on maximum
germination rate
), but with a cap on maximum
germination rate  , to prevent excessive dominance
of one plant functional type over the seed pool.
, to prevent excessive dominance
of one plant functional type over the seed pool.

Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Maximum seed mass |
kgC m |
|
|
Proportional germination rate |
none |
|
|
Maximum germination rate |
KgC
m y |
|
|
Decay rate of viable seeds |
none |
ft |
|
Fraction of
|
none |
ft |
1.14.1. Environmentally Sensitive Tree Recruitment¶
FATES has the option to represent environmentally sensitive tree recruitment using the Tree Recruitment Scheme (TRS), a module that was originally presented offline of FATES (Hanbury-Brown et al. 2022). The primary goal of the TRS is to more mechanistically constrain the amount of carbon available for recruitment based on conditions at the forest floor.
The TRS is off by default (fates_regeneration_model = 1), but can be switched on using the parameter file. The TRS can be switched on in a reduced complexity mode (fates_regeneration_model = 3) without seedling dynamics where it represents 1) pft-specific reproductive allocation schedules as a function of dbh and 2) allocation to non-seed reproductive biomass. If the TRS is switched on with seedling dynamics (fates_regeneration_model = 2) it will also represent environmentally sensitive seedling emergence, seedling mortality and transition into the sapling stage (i.e. cohorts tracked by FATES).
The TRS allocates a dynamic fraction of carbon for growth and reproduction
( ; positive carbon balance net after tissue turnover and allocation
to storage) to reproduction. Regeneration processes, described in detail below,
move dynamic fractions of
; positive carbon balance net after tissue turnover and allocation
to storage) to reproduction. Regeneration processes, described in detail below,
move dynamic fractions of  through a seedbank and seedling pool
which are tracked in units of carbon. Carbon recruiting out of the seedling pool
each day is passed back to FATES’s default recruitment subroutine. The TRS determines
how much carbon is available for recruitment and FATES’s recruitment subroutine calculates
how many new recruits to produce and initializes the new cohort. Carbon in seeds or
seedlings that die or that is allocated to non-seed reproductive biomass, moves to the
litter pool. Unlike the offline version of the TRS presented in
Hanbury-Brown et al. (2022), FATES-TRS uses
exponential moving averages (EMAs) of environmental variables in the seedling
layer to calculate the rates of regeneration processes.
EMAs are tracked on different timescales depending on the process.
through a seedbank and seedling pool
which are tracked in units of carbon. Carbon recruiting out of the seedling pool
each day is passed back to FATES’s default recruitment subroutine. The TRS determines
how much carbon is available for recruitment and FATES’s recruitment subroutine calculates
how many new recruits to produce and initializes the new cohort. Carbon in seeds or
seedlings that die or that is allocated to non-seed reproductive biomass, moves to the
litter pool. Unlike the offline version of the TRS presented in
Hanbury-Brown et al. (2022), FATES-TRS uses
exponential moving averages (EMAs) of environmental variables in the seedling
layer to calculate the rates of regeneration processes.
EMAs are tracked on different timescales depending on the process.

Figure 1.1 Daily regeneration processes (depicted with hour glasses) represented by FATES-TRS transfer reproductive carbon through seed bank and seedling carbon pools (depicted as circles). Processes are sensitive to DBH or environmental conditions (see inset key). The litter pool receives non-seed reproductive carbon, dead seeds, and dead seedlings. Carbon for new recruits is passed back to FATES’s default recruitment subroutine. “Host VDM” = FATES.¶
1.14.1.1. Allocation to reproduction¶
Allocation to reproduction occurs in FATES’s parteh module (parteh/PRTAllometricCarbonMod.F90).
FATES without the TRS switched on (i.e. “default FATES”) assumes reproductive allocation is either
insensitive to size or is a step function of size, depending on the parameterization. In contrast,
the TRS allocates a dynamic fraction of cohort-level  to reproduction based on the
cohort’s size and the TRS’s reproductive allocation (RA)
function. This follows observations that the probability a tree is
reproductive increases sigmoidally with size within species (Visser et al., 2016).
Each mature cohort contributes to recruitment via the TRS if they are in positive carbon balance.
The effective fraction of cohort-level
to reproduction based on the
cohort’s size and the TRS’s reproductive allocation (RA)
function. This follows observations that the probability a tree is
reproductive increases sigmoidally with size within species (Visser et al., 2016).
Each mature cohort contributes to recruitment via the TRS if they are in positive carbon balance.
The effective fraction of cohort-level 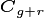 allocated to reproduction,
allocated to reproduction,  ,
is calculated based on a sigmoidal relationship relating the cohort’s current dbh (cm)
to the probability of being reproductive (
,
is calculated based on a sigmoidal relationship relating the cohort’s current dbh (cm)
to the probability of being reproductive ( ). This formulation assumes
that all reproductive individuals in a cohort allocate to reproduction at a constant, PFT-specific rate,
). This formulation assumes
that all reproductive individuals in a cohort allocate to reproduction at a constant, PFT-specific rate,
 , which is modified by
, which is modified by  to calculate
to calculate 
(1.47)¶
(1.48)¶
where  and
and 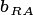 are PFT-specific parameters describing the shape of the sigmoidal curve.
This functional form is consistent with empirical data (Visser et al., 2016;
Minor & Kobe, 2019). The TRS subsequently multiplies
are PFT-specific parameters describing the shape of the sigmoidal curve.
This functional form is consistent with empirical data (Visser et al., 2016;
Minor & Kobe, 2019). The TRS subsequently multiplies  by
by 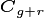 to get reproductive carbon per cohort.
to get reproductive carbon per cohort.
See Table below for all TRS parameters.
1.14.1.2. Allocation to seed vs. non-seed reproductive biomass and seed mortality¶
In nature, only a subset of the carbon allocated to reproduction becomes seeds, with the rest going to flowers,
fruit flesh, capsules, etc. (Wenk et al., 2017). Default FATES sends all reproductive carbon
to an undifferentiated “seed pool” from which carbon is lost and recruits are formed
(Fisher et al., 2015). The TRS partitions each cohort’s reproductive carbon into seed carbon
and non-seed reproductive carbon (e.g., flowers, fruit flesh, and capsules) based on a prescribed,
PFT-specific fraction of reproductive carbon that is seed,  . This happens in the SeedIn
subroutine (biogeochem/EDPhysiologyMod). Seed carbon moves to the seed bank each day and non-seed reproductive
carbon moves to litter. Seeds in the seed bank die at a PFT-specific, constant rate,
. This happens in the SeedIn
subroutine (biogeochem/EDPhysiologyMod). Seed carbon moves to the seed bank each day and non-seed reproductive
carbon moves to litter. Seeds in the seed bank die at a PFT-specific, constant rate,  ,
which represents all modes of seed mortality including predation and decay (same as default FATES).
,
which represents all modes of seed mortality including predation and decay (same as default FATES).
1.14.1.3. Seedling emergence¶
Seedling emergence is sensitive to soil moisture (Garwood, 1983; Atondo-Bueno et al., 2016; Ruiz Talonia et al., 2017) and light (Pearson et al., 2002) in nature. Default FATES represents it as an environmentally insensitive constant. In the TRS, emergence depends on both soil moisture and light.
Light-dependence of germination is captured on day i in a Michaelis-Menten rate modifier [0,1]

based on  , the 24-hour EMA of photosynthetically active radiation (PAR) at the seedling layer.
Seedling layer PAR is sensitive to canopy layer and understory layer vegetation cover such that seedling layer PAR is an area-weighted average of PAR incident at the top and bottom of the understory layer. When there is very little
vegetation present, PAR at the seedling layer is taken from the boundary conditions (i.e. same as top of canopy).
, the 24-hour EMA of photosynthetically active radiation (PAR) at the seedling layer.
Seedling layer PAR is sensitive to canopy layer and understory layer vegetation cover such that seedling layer PAR is an area-weighted average of PAR incident at the top and bottom of the understory layer. When there is very little
vegetation present, PAR at the seedling layer is taken from the boundary conditions (i.e. same as top of canopy).
 is a PFT-specific PAR threshold governing the shape of the germination response to reduced light.
Most tropical pioneer species exhibit an increase in germination probability with increases in light,
whereas germination in shade-tolerant species is insensitive to light (captured by
is a PFT-specific PAR threshold governing the shape of the germination response to reduced light.
Most tropical pioneer species exhibit an increase in germination probability with increases in light,
whereas germination in shade-tolerant species is insensitive to light (captured by  ).
).
The EMA of soil matric potential on day i ( ) at seedling rooting depth,
) at seedling rooting depth, 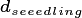 ,
is influenced by SMP in a rolling window of days,
,
is influenced by SMP in a rolling window of days,  (default = 7 days),
prior to i. If
(default = 7 days),
prior to i. If  is above a critical threshold,
is above a critical threshold,  , then seedling emergence occurs.
The emergence rate on day i,
, then seedling emergence occurs.
The emergence rate on day i,  , is dynamically calculated as a function of
, is dynamically calculated as a function of  .
The pft-specific moisture response parameter,
.
The pft-specific moisture response parameter,  , modifies the mean seedling emergence coefficient
(
, modifies the mean seedling emergence coefficient
( ) in response to variation in
) in response to variation in  such that
such that

This produces pulses of seedling emergence in response to seasonal and interannual precipitation events, and stalls seedling emergence under relatively dry conditions.
1.14.1.4. Moisture and light-sensitive seedling survival¶
The TRS tracks a seedling pool that is sensitive to light and moisture stress. Seedling survival decreases differentially at low soil moisture and low light, affecting forest composition across environmental gradients (Kobe, 1999; Engelbrecht et al., 2007).
The TRS seeks to capture this with a PFT-specific moisture stress threshold,  ,
below which the seedling pool starts to “accumulate” (mathematically an EMA is tracked with a
timescale of
,
below which the seedling pool starts to “accumulate” (mathematically an EMA is tracked with a
timescale of  days; default = 126) moisture deficit days (MDD) similar to the concept
of growing degree days. The new MDD value on day i,
days; default = 126) moisture deficit days (MDD) similar to the concept
of growing degree days. The new MDD value on day i,  , is calculated as the difference
between the absolute value of site-level SMP on day i,
, is calculated as the difference
between the absolute value of site-level SMP on day i,  , and the absolute value of
, and the absolute value of  .
.
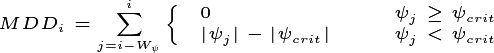
 is then used to update an EMA of MDD,
is then used to update an EMA of MDD,  . Finally,
. Finally,  is
multiplied by the timescale of the EMA (in days),
is
multiplied by the timescale of the EMA (in days),  , to approximate an “accumulation” of MDD.
, to approximate an “accumulation” of MDD.
This formulation simultaneously captures the magnitude and duration of moisture stress.
Observations of seedling wilting points from a manipulative drought experiment at BCI
(Engelbrecht & Kursar, 2003; Engelbrecht et al., 2007)
were used to explore the relationship between MDD accumulation and seedling mortality.
Observed drought-induced mortality is 0 up to a critical accumulation of MDD,  ,
at which point a convex quadratic relationship best explained drought-induced seedling mortality as a function of MDD
(see SI Methods S1 and Fig. S1 in Hanbury-Brown et al., 2022 for more details).
The mortality rate from moisture stress (
,
at which point a convex quadratic relationship best explained drought-induced seedling mortality as a function of MDD
(see SI Methods S1 and Fig. S1 in Hanbury-Brown et al., 2022 for more details).
The mortality rate from moisture stress ( ) on day i is therefore
) on day i is therefore

Seedlings also die from insufficient light, which we refer to as light stress. The light stress mortality rate,
 , on day i is a function of “cumulative” (mathematically an EMA is tracked with a timescale of W_L days; default = 32) PAR at the seedling layer,
, on day i is a function of “cumulative” (mathematically an EMA is tracked with a timescale of W_L days; default = 32) PAR at the seedling layer,  , within a moving window of days,
, within a moving window of days,  , prior to i. Similar to the approach used to calculate
, prior to i. Similar to the approach used to calculate  ,
,  is calculated by multiplying an EMA of seedling layer PAR,
is calculated by multiplying an EMA of seedling layer PAR,  , by
, by  to approximate the cumulative light incident at the seedling layer prior to i. Two PFT-specific parameters determine the shape of the negative exponential relationship between mortality and and light
to approximate the cumulative light incident at the seedling layer prior to i. Two PFT-specific parameters determine the shape of the negative exponential relationship between mortality and and light

where  is a PFT-specific light response parameter and
is a PFT-specific light response parameter and  is the intercept. This function is based on an analysis by Kobe (1999) who tested four functional forms and found that the negative exponential best described light stress mortality for two shade tolerant and one light demanding species that were transplanted into varied light environments. A background seedling mortality rate,
is the intercept. This function is based on an analysis by Kobe (1999) who tested four functional forms and found that the negative exponential best described light stress mortality for two shade tolerant and one light demanding species that were transplanted into varied light environments. A background seedling mortality rate,  , represents other seedling mortality (e.g. herbivory, pathogens, tree fall, etc.). Total seedling mortality is the sum of moisture-dependent, light-dependent and background mortality.
, represents other seedling mortality (e.g. herbivory, pathogens, tree fall, etc.). Total seedling mortality is the sum of moisture-dependent, light-dependent and background mortality.
1.14.1.5. Recruitment¶
The rate of transition from seedling to sapling increases with understory light (Brokaw, 1985; Rüger et al., 2009b). Recruitment in the TRS is represented with a dynamic seedling to sapling transition rate (TR) which is the fraction of total carbon in the seedling pool,  , that is available to make new recruits each day. The TR on day i is calculated as a power function of
, that is available to make new recruits each day. The TR on day i is calculated as a power function of  . If SMP on day i,
. If SMP on day i,  , is drier than
, is drier than  the transition rate goes to zero such that
the transition rate goes to zero such that

where  is a coefficient derived from the mean transition rate at observed mean understory PAR (see SI Methods S1 in Hanbury-Brown et al. (2022) for more information) and
is a coefficient derived from the mean transition rate at observed mean understory PAR (see SI Methods S1 in Hanbury-Brown et al. (2022) for more information) and  is the light response modifier. The light response modifier produces accelerating (i.e. light demanding) or decelerating responses to light (Fig. 2f) depending on if
is the light response modifier. The light response modifier produces accelerating (i.e. light demanding) or decelerating responses to light (Fig. 2f) depending on if  is greater or less than 1. Of a variety of functional forms tested at BCI, a power function with species-specific light response modifiers best explained observed variation in recruitment rates under spatially heterogenous patch-level light (Rüger et al., 2009). This formulation is more broadly supported by the growth-mortality functional trade-off axis where light demanding species can take advantage of higher light conditions through faster relative growth rates (Wright et al., 2010).
is greater or less than 1. Of a variety of functional forms tested at BCI, a power function with species-specific light response modifiers best explained observed variation in recruitment rates under spatially heterogenous patch-level light (Rüger et al., 2009). This formulation is more broadly supported by the growth-mortality functional trade-off axis where light demanding species can take advantage of higher light conditions through faster relative growth rates (Wright et al., 2010).
Carbon transitioning out of the seedling layer is available to FATES’s default recruitment subroutine which converts carbon available for recruitment into a number density of new recruits based on the amount of carbon required to form an individual in the smallest size class tracked by the VDM, Z0. The number of new recruits predicted on day i,  , is
, is

The regeneration processes represented above introduce 18 new parameters used by FATES-TRS that are not used by default FATES.
Parameter symbol and full parameter name |
Value optimized for BCI |
Units |
Description |
|---|---|---|---|
|
0.1 (all PFTs) |
None |
Fraction of |
|
LD-DI: 0.0058 LD-DT: 0.0059 ST-DI: 0.0042 ST-DT: 0.0049 |
|
Governs RA as function of dbh (logit function coefficient) |
|
LD-DI: -3.1380 LD-DT: -2.4607 ST-DI: -2.6518 ST-DT: -2.6171 |
None |
Governs RA as function of dbh (intercept in logit function) |
|
0.24 (all PFTs) |
None |
Fraction of reproductive C that is seed |
|
0.51 (all PFTs) |
yr-1 |
Seed mortality rate |
|
0.06 (all PFTs) |
m |
Seedling rooting depth |
|
0.0003 |
day-1 |
Coefficient for seedling emergence rate |
|
LD-DI: 1.6 LD-DT: 1.6 ST-DI: 1.2 ST-DT: 1.2 |
None |
Seedling emergence sensitivity to soil moisture |
|
7 (all PFTs) |
days |
Time window for emergence response to soil moisture |
|
-15744.65 |
mm H2O suction |
Soil moisture required for emergence |
|
0.656 |
MJ m-2 day-1 |
Critical PAR level for light-sensitive germination |
|
LD-DI: 0.17 LD-DT: 0.18 ST-DI: 0.19 ST-DT: 0.11 |
yr-1 |
Background seedling mortality rate |
|
DI: -175912.9 DT: -251995.7 |
mm H2O suction |
Seedling moisture stress threshold |
|
DI: 46E5 DT: 14E5 |
mm H2O suction days |
Moisture deficit day threshold for seedling mortality |
|
DI: 1.04E-16 DT: 4.07E-17 |
None |
Moisture-based mortality coefficient |
|
DI:-5.5E-10 DT:-6.4E-11 |
None |
Moisture-based mortality coefficient |
|
DI:3.5E-04 DT:1.3E-05 |
None |
Moisture-based mortality coefficient |
(fates_trs_sdlng_mdd_timescale) |
126 (all PFTs) |
days |
Time window for MDD |
(fates_trs_seedling_light_mort_a) |
LD:-0.033 ST:-0.00990 |
None |
Light-based mortality coefficient |
(fates_trs_seedling_light_mort_b) |
LD:-3.84 ST:-7.15 |
None |
Light-based mortality coefficient |
(fates_trs_sdlng_mort_par_timescale) |
32 (all PFTs) |
days |
Time window for seedling light response |
(fates_trs_seedling_light_rec_a) |
LD:0.010 ST:0.007 |
None |
Seedling to sapling transition rate coefficient |
(fates_trs_seedling_light_rec_b) |
LD: 1.0653 ST: 0.8615 |
None |
Recruitment light response parameter |
|
2.345 |
m |
Min height of a new recruit |
fates_trs_regeneration_model |
2 |
None |
Switch to choose regeneration mode (1: default FATES 2: TRS 3: TRS no seedling dynamics) |
1.15. Litter Production and Fragmentation¶
 ,
,  ) and leaf
litter (
) and leaf
litter ( and fine root litter
and fine root litter  ). All
pools are represented per patch, and with units of kGC
m
). All
pools are represented per patch, and with units of kGC
m . Further to this,
. Further to this,  ,
,  are split into four litter size classes (
are split into four litter size classes ( ) for the purposes
of proscribing this to the SPITFIRE fire model (seed ’Fuel Load’
section for more detail. 1-hour (twigs), 10-hour (small branches),
100-hour (large branches) and 1000-hour(boles or trunks). 4.5 %, 7.5%,
21 % and 67% of the woody biomass (
) for the purposes
of proscribing this to the SPITFIRE fire model (seed ’Fuel Load’
section for more detail. 1-hour (twigs), 10-hour (small branches),
100-hour (large branches) and 1000-hour(boles or trunks). 4.5 %, 7.5%,
21 % and 67% of the woody biomass ( )
is partitioned into each class, respectively. If the cohort dbh is smaller
than the fuel class size threshold specified by the fates_frag_cwd_frac
parameter then no biomass is sent to that class. The relative
proportions of biomass sent to each of the remaining fuel classes are preserved.
)
is partitioned into each class, respectively. If the cohort dbh is smaller
than the fuel class size threshold specified by the fates_frag_cwd_frac
parameter then no biomass is sent to that class. The relative
proportions of biomass sent to each of the remaining fuel classes are preserved. and
and  are indexed by plant functional
type (
are indexed by plant functional
type ( ). The rational for indexing leaf and fine root by PFT
is that leaf and fine root matter typically vary in their
carbon:nitrogen ratio, whereas woody pools typically do not.
). The rational for indexing leaf and fine root by PFT
is that leaf and fine root matter typically vary in their
carbon:nitrogen ratio, whereas woody pools typically do not.
Rates of change of litter, all in kGC m year
year , are calculated as
, are calculated as

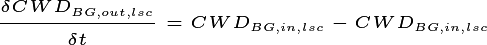


1.15.1. Litter Inputs¶
Inputs into the litter pools come from tissue turnover, mortality of canopy trees, mortality of understorey trees, mortality of seeds, and leaf senescence of deciduous plants.

where  is the leaf turnover rate for evergreen trees
and
is the leaf turnover rate for evergreen trees
and  is the leaf loss from phenology in that
timestep (KgC
is the leaf loss from phenology in that
timestep (KgC  .
.  is the total mortality
flux in that timestep (in individuals). For fine root input.
is the total mortality
flux in that timestep (in individuals). For fine root input.
 is the number of cohorts of functional type
‘
is the number of cohorts of functional type
‘ ’ in the current patch.
’ in the current patch.

where  is the root turnover rate. For coarse woody
debris input (
is the root turnover rate. For coarse woody
debris input ( , we first calculate the
sum of the mortality
, we first calculate the
sum of the mortality  and
turnover
and
turnover  ) fluxes, then separate these into
size classes and above/below ground fractions using the fixed fractions
assigned to each (
) fluxes, then separate these into
size classes and above/below ground fractions using the fixed fractions
assigned to each ( and
and  )
)


1.15.2. Litter Outputs¶
The fragmenting litter pool is available for burning but not for
respiration or decomposition. Fragmentation rates are calculated
according to a maximum fragmentation rate ( or
or
 ) which is ameliorated by a temperature and water
dependent scalar
) which is ameliorated by a temperature and water
dependent scalar  . The form of the temperature scalar is
taken from the existing CLM4.5BGC decomposition cascade calculations).
The water scaler is equal to the water limitation on photosynthesis
(since the CLM4.5BGC water scaler pertains to the water potential of
individual soil layers, which it is difficult to meaningfully average,
given the non-linearities in the impact of soil moisture). The scaler
code is modular, and new functions may be implemented trivially. Rate
constants for the decay of the litter pools are extremely uncertain in
literature, as few studies either separate litter into size classes, nor
examine its decomposition under non-limiting moisture and temperature
conditions. Thus, these parameters should be considered as part of
sensitivity analyses of the model outputs.
. The form of the temperature scalar is
taken from the existing CLM4.5BGC decomposition cascade calculations).
The water scaler is equal to the water limitation on photosynthesis
(since the CLM4.5BGC water scaler pertains to the water potential of
individual soil layers, which it is difficult to meaningfully average,
given the non-linearities in the impact of soil moisture). The scaler
code is modular, and new functions may be implemented trivially. Rate
constants for the decay of the litter pools are extremely uncertain in
literature, as few studies either separate litter into size classes, nor
examine its decomposition under non-limiting moisture and temperature
conditions. Thus, these parameters should be considered as part of
sensitivity analyses of the model outputs.




1.15.3. Flux into decompsition cascade¶
Upon fragmentation and release from the litter pool, carbon is
transferred into the labile, lignin and cellulose decomposition pools.
These pools are vertically resolved in the biogeochemistry model. The
movement of carbon into each vertical layer is obviously different for
above- and below-ground fragmenting pools. For each layer  and
chemical litter type
and
chemical litter type  , we derive a flux from ED into the
decomposition cascade as
, we derive a flux from ED into the
decomposition cascade as  (kGC m
(kGC m s
s )
)
where  is the time conversion factor from years to seconds,
is the time conversion factor from years to seconds,
 ,
,  and
and  are the
fractions of labile, cellulose and lignin in leaf litter, and
are the
fractions of labile, cellulose and lignin in leaf litter, and
 ,
,  and
and  are their
counterparts for root matter. Similarly,
are their
counterparts for root matter. Similarly,  ,
,
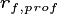 and
and  are the fractions of leaf,
coarse root and fine root matter that are passed into each vertical soil
layer
are the fractions of leaf,
coarse root and fine root matter that are passed into each vertical soil
layer  , derived from the CLM(BGC) model.
, derived from the CLM(BGC) model.
Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Maximum fragmentation rate of CWD |
y |
|
|
Maximum fragmentation rate of leaf litter |
y |
|
|
Maximum fragmentation rate of fine root litter |
y |
|
|
Fraction of leaf mass in labile carbon pool |
none |
|
|
Fraction of leaf mass in cellulose carbon pool |
none |
|
|
Fraction of leaf mass in lignin carbon pool |
none |
|
|
Fraction of root mass in labile carbon pool |
none |
|
|
Fraction of root mass in cellulose carbon pool |
none |
|
|
Fraction of root mass in lignin carbon pool |
none |
|
|
Fraction of leaf matter directed to soil layer z |
none |
soil layer |
|
Fraction of coarse root matter directed to soil layer z |
none |
soil layer |
|
Fraction of fine root matter directed to soil layer z |
none |
soil layer |
1.16. Disturbance¶
FATES allows disturbance through three processes: (1) mortality of
canopy trees, (2) fire, (3) anthropogenic disturbance. Each of these
is discussed in more detail below. For the case of canopy tree
mortality, some fraction of the crown area  of deceased trees is used
to generate newly-disturbed patch area, while the rest
of deceased trees is used
to generate newly-disturbed patch area, while the rest  remains in
the existing patch. Thus varying
remains in
the existing patch. Thus varying  from zero to 1 can lead
to three different cases of how mortlaity leads to disturbance. If
from zero to 1 can lead
to three different cases of how mortlaity leads to disturbance. If
 , then all canopy area is converted into newly-disturbed
patch area, and a fraction of understory trees equal to the ratio of
dying-tree crown are a to the patches area are moved to the newly-disturbed patch, at
which time they are promoted to the canopy of the new patch; this is
labeled below as the ‘Pure ED’ case. For those trees that are moved
to the new patch, some fraction of these will die due to impacts from
the disturbance process itself, this fraction
, then all canopy area is converted into newly-disturbed
patch area, and a fraction of understory trees equal to the ratio of
dying-tree crown are a to the patches area are moved to the newly-disturbed patch, at
which time they are promoted to the canopy of the new patch; this is
labeled below as the ‘Pure ED’ case. For those trees that are moved
to the new patch, some fraction of these will die due to impacts from
the disturbance process itself, this fraction  is currently
a global parameter for all individual-tree disturbance processes, with
a default value of 0.55983. If
is currently
a global parameter for all individual-tree disturbance processes, with
a default value of 0.55983. If
 , then no disturbance occurs and all mortality is
accomodated by promotion of trees from the understory to the canopy
within a patch; this is the structure of the PPA formulation as
described in Purves et al. 2008, and is labelled
below as ‘Pure PPA’. If
, then no disturbance occurs and all mortality is
accomodated by promotion of trees from the understory to the canopy
within a patch; this is the structure of the PPA formulation as
described in Purves et al. 2008, and is labelled
below as ‘Pure PPA’. If  , then some both processes of
promotion within a patch and promotion into a new patch occur. A
special case of this is when all trees that would be moved into the
new patch are killed in the process, thus guaranteeing that
newly-disturbed patches are devoid of any surviving trees; this is
blabelled below as the ‘bare-ground intermediate case’.
, then some both processes of
promotion within a patch and promotion into a new patch occur. A
special case of this is when all trees that would be moved into the
new patch are killed in the process, thus guaranteeing that
newly-disturbed patches are devoid of any surviving trees; this is
blabelled below as the ‘bare-ground intermediate case’.
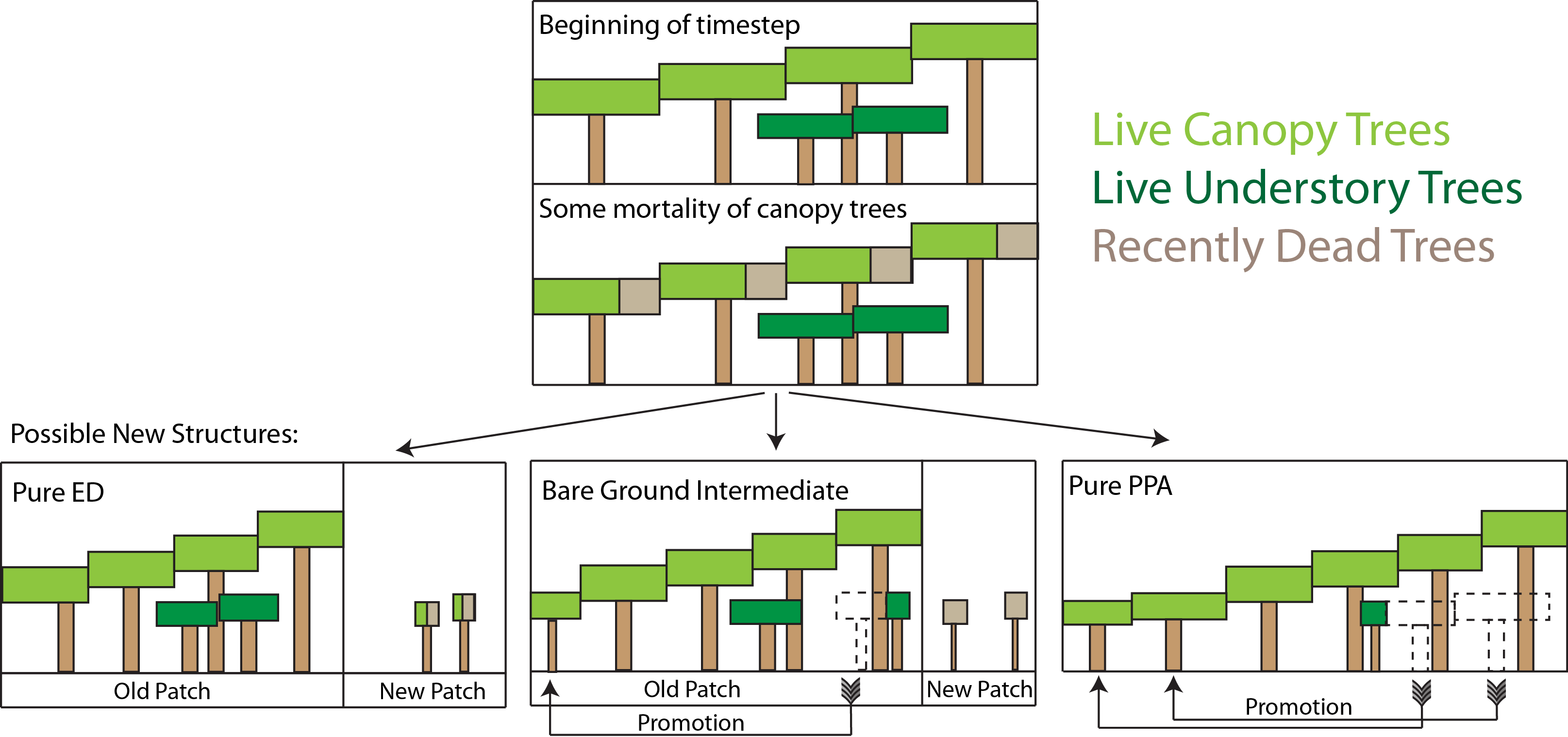
1.17. Plant Mortality¶
Total plant mortality per cohort  , (fraction
year
, (fraction
year ) is simulated as the sum of several additive terms,
) is simulated as the sum of several additive terms,

where  is the background mortality that is unaccounted by
any of the other mortality rates and is fixed at a constant
PFT-dependent rate in the parameter file.
is the background mortality that is unaccounted by
any of the other mortality rates and is fixed at a constant
PFT-dependent rate in the parameter file.
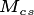 is the carbon starvation derived mortality, which is a function of the
non-structural carbon storage term
is the carbon starvation derived mortality, which is a function of the
non-structural carbon storage term  and the
‘target’ leaf biomass,
and the
‘target’ leaf biomass,  , as follows:
, as follows:

where  is the maximum rate of carbon storage mortality parameter, or the
maximum rate of trees in a landscape that will die when their carbon
stores are exhausted. This parameter is needed to scale from
individual-level mortality simulation to grid-cell average conditions.
is the maximum rate of carbon storage mortality parameter, or the
maximum rate of trees in a landscape that will die when their carbon
stores are exhausted. This parameter is needed to scale from
individual-level mortality simulation to grid-cell average conditions.
Thus FATES implicitly assumes that there is a critical storage
pool  that sets the
total-plant storage level where mortality begins; the implied
parameter
that sets the
total-plant storage level where mortality begins; the implied
parameter  could be made explicit, but we left this as an
implicit parameter here due to the generally weak data constraints on
it at present. Because both the increase in mortality and the decrease
in respiration (see section ‘Respiration’) begin when
could be made explicit, but we left this as an
implicit parameter here due to the generally weak data constraints on
it at present. Because both the increase in mortality and the decrease
in respiration (see section ‘Respiration’) begin when  drops below
drops below  , and
, and  , the parameter
, the parameter
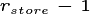 , thus sets the size of the carbon
storage buffer that determines how much cumulative negative NPP a
plant can experience before it begins to suffer from carbon
starvation.
, thus sets the size of the carbon
storage buffer that determines how much cumulative negative NPP a
plant can experience before it begins to suffer from carbon
starvation.
Mechanistic simulation of hydraulic failure is not undertaken on account
of it’s mechanistic complexity (see McDowell et al. 2013 for
details). Instead, we use a proxy for hydraulic failure induced
mortality ( ) that uses a water potential threshold
beyond which mortality is triggered, such that the tolerance of low water
potentials is a function of plant functional type (as expressed via the
) that uses a water potential threshold
beyond which mortality is triggered, such that the tolerance of low water
potentials is a function of plant functional type (as expressed via the
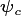 parameter). For each day that the aggregate water
potential falls below a threshold value, a set fraction of the trees are
killed. To prevent hydraulic failure mortality of vegetation at high latitudes,
parameter). For each day that the aggregate water
potential falls below a threshold value, a set fraction of the trees are
killed. To prevent hydraulic failure mortality of vegetation at high latitudes,
 when the temperature of any soil layer (
when the temperature of any soil layer ( ) falls below -2 degrees C.
The aggregation of soil moisture potential across the root zone
is expressed using the
) falls below -2 degrees C.
The aggregation of soil moisture potential across the root zone
is expressed using the 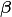 function. We thus determine plant
mortality caused by extremely low water potentials as
function. We thus determine plant
mortality caused by extremely low water potentials as

The threshold value of 10 represents a state where the
average soil moisture potential is within 10
represents a state where the
average soil moisture potential is within 10 of the
wilting point (a PFT specific parameter
of the
wilting point (a PFT specific parameter  ).
).
 is the fire-induced mortality, as described in the
fire modelling section.
is the fire-induced mortality, as described in the
fire modelling section.
Impact mortality M_{i,coh} occurs to understory trees that are kille dduring the process of disturbance, as described above.
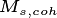 and
and  are size- and age-dependent mortality respectively. These terms model a gradual increase in mortality rate with either cohort DBH (cm) or cohort age. We model
are size- and age-dependent mortality respectively. These terms model a gradual increase in mortality rate with either cohort DBH (cm) or cohort age. We model 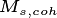 as:
as:

where  is diameter at breast height in cm,
is diameter at breast height in cm,  is the rate that mortality increases with DBH, and
is the rate that mortality increases with DBH, and  is the inflection point of the curve, i.e. the DBH at which annual mortality rate has increased to 50%. We model
is the inflection point of the curve, i.e. the DBH at which annual mortality rate has increased to 50%. We model  as :
as :
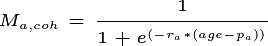
where  is cohort age in years,
is cohort age in years,  is the rate that mortality increases with age, and
is the rate that mortality increases with age, and  is the inflection point of the curve, i.e. the age at which annual mortality rate has increased to 50%.
is the inflection point of the curve, i.e. the age at which annual mortality rate has increased to 50%.
Cohort age is not tracked in default FATES. In order to have age-dependent mortality on, set the flag use_fates_cohort_age_tracking to .true. in the FATES namelist options. To turn on either size- or age-dependent mortality set the  and
and 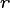 parameters to sensible values in the FATES parameter file.
parameters to sensible values in the FATES parameter file.
Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Stress Mortality Scaler |
none |
|
|
Target carbon storage fraction |
none |
ft |
1.18. Fire (SPITFIRE)¶
The influence of fire on vegetation is estimated using the SPITFIRE model, which has been modified for use in ED following it’s original implementation in the LPJ-SPITFIRE model (Thonicke et al. 2010, Pfeiffer et al. 2013). This model as described is substantially different from the existing CLM4.5 fire model Li et al. 2012, however, further developments are intended to increase the merging of SPITFIRE’s natural vegetation fire scheme with the fire suppression, forest-clearing and peat fire estimations in the existing model. The coupling to the ED model allows fires to interact with vegetation in a size-structured manner, so small fires can burn only understorey vegetation. Also, the patch structure and representation of succession in the ED model allows the model to track the impacts of fire on different forest stands, therefore removing the problem of area-averaging implicit in area-based DGVMs. The SPITFIRE approach has also been coupled to the LPJ-GUESS individual-based model (Forrest et al. in prep) and so this is not the only implementation of this type of scheme in existence.
The SPITFIRE model operates at a daily timestep and at the patch level, meaning that different litter pools and vegetation charecteristics of open and closed forests can be represented effectively (we omit the patch subscript throughout for simplicity).
1.18.1. Properties of fuel load¶
Many fire processes are impacted by the properties of the litter pool in the SPITFIRE model. There are one live (live grasses) and five dead fuel categories (dead leaf litter and four pools of coarse woody debris). Coarse woody debris is classified into 1h, 10h, 100h, and 1000h fuels, defined by the order of magnitude of time required for fuel to lose (or gain) 63% of the difference between its current moisture content and the equilibrium moisture content under defined atmospheric conditions. Thonicke et al. 2010. For the purposes of describing the behaviour of fire, we introduce a new index ‘fuel class’ fc, the values of which correspond to each of the six possible fuel categories as follows.
fc index |
Fuel type |
Drying Time |
|---|---|---|
1 |
dead grass |
n/a |
2 |
twigs |
1h fuels |
3 |
small branches |
10h fuel |
4 |
large branches |
100h fuel |
5 |
stems and trunks |
1000h fuel |
6 |
live grasses |
n/a |
1.18.2. Nesterov Index¶
Dead fuel moisture ( ), and several other
properties of fire behaviour, are a function of the ‘Nesterov Index’
(
), and several other
properties of fire behaviour, are a function of the ‘Nesterov Index’
( ) which is an accumulation over time of a function of
temperature and humidity (Eqn 5, Thonicke et al. 2010),
) which is an accumulation over time of a function of
temperature and humidity (Eqn 5, Thonicke et al. 2010),

where  is the daily mean temperature in
is the daily mean temperature in  C and
C and
 is the dew point calculated as .
is the dew point calculated as .

where  is the relative humidity (%).
is the relative humidity (%).
On days when the total precipitation exceeds 3.0mm, the Nesterov index accumulator is reset back to zero.
1.18.3. Fuel properties¶
Total fuel load  for a given patch is the sum of
the above ground coarse woody debris and the leaf litter, plus the alive
grass leaf biomass
for a given patch is the sum of
the above ground coarse woody debris and the leaf litter, plus the alive
grass leaf biomass  multiplied by the non-mineral
fraction (1-
multiplied by the non-mineral
fraction (1- ).
).

Many of the model behaviours are affected by the patch-level weighted average properties of the fuel load. Typically, these are calculated in the absence of 1000-h fuels because these do not contribute greatly to fire spread properties.
1.18.3.1. Dead Fuel Moisture Content¶
Dead fuel moisture is calculated as

where  is a parameter defining how fuel moisture
content varies between the first four dead fuel classes.
is a parameter defining how fuel moisture
content varies between the first four dead fuel classes.
1.18.3.2. Live grass moisture Content¶
The live grass fractional moisture content( )
is a function of the soil moisture content. (Equation B2 in
Thonicke et al. 2010)
)
is a function of the soil moisture content. (Equation B2 in
Thonicke et al. 2010)
where  is the fractional moisture content of the top
30cm of soil.
is the fractional moisture content of the top
30cm of soil.
1.18.3.3. Patch Fuel Moisture¶
The total patch fuel moisture is based on the weighted average of the different moisture contents associated with each of the different live grass and dead fuel types available (except 1000-h fuels).

1.18.3.4. Effective Fuel Moisture Content¶
Effective Fuel Moisture Content is used for calculations of fuel
consumed, and is a function of the ratio of dead fuel moisture content
 and the moisture of extinction factor,
and the moisture of extinction factor,


where the  is a function of surface-area to volume ratio.
is a function of surface-area to volume ratio.
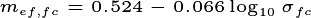
1.18.3.5. Patch Fuel Moisture of Extinction¶
The patch ‘moisture of extinction’ factor ( ) is the
weighted average of the
) is the
weighted average of the  of the different fuel classes
of the different fuel classes

1.18.3.6. Patch Fuel Bulk Density¶
The patch fuel bulk density is the weighted average of the bulk density of the different fuel classes (except 1000-h fuels).

where  is the bulk density of each fuel size
class (kG m
is the bulk density of each fuel size
class (kG m )
)
1.18.3.7. Patch Fuel Surface Area to Volume¶
The patch surface area to volume ratio ( ) is the
weighted average of the surface area to volume ratios
(
) is the
weighted average of the surface area to volume ratios
( ) of the different fuel classes (except 1000-h
fuels).
) of the different fuel classes (except 1000-h
fuels).

1.18.4. Forward rate of spread¶
For each patch and each day, we calculate the rate of forward spread of
the fire ros (nominally in the direction of the wind).
(nominally in the direction of the wind).

 is the effective heating number
(
is the effective heating number
( ).
).  is the
heat of pre-ignition (
is the
heat of pre-ignition ( ).
).  is the
propagating flux calculated as (see Thonicke et al. 2010
Appendix A).
is the
propagating flux calculated as (see Thonicke et al. 2010
Appendix A).

 is the influence of windspeed on rate of spread.
is the influence of windspeed on rate of spread.

Where  ,
,  and
and  are all functions of
surface-area-volume ratio
are all functions of
surface-area-volume ratio  :
:
 ,
,
 ,
,
 .
.  where
where
 is the the windspeed in ms
is the the windspeed in ms , and
, and
 where
where  is the particle density (513).
is the particle density (513).
 is the reaction intensity, calculated using the following
set of expressions (from Thonicke et al. 2010 Appendix A).:
is the reaction intensity, calculated using the following
set of expressions (from Thonicke et al. 2010 Appendix A).:

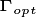 is the residence time of the fire, and
is the residence time of the fire, and
 is the mineral damping coefficient
(=0.174
is the mineral damping coefficient
(=0.174 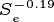 , where
, where  is 0.01 and so =
is 0.01 and so =
 0.41739).
0.41739).
1.18.5. Fuel Consumption¶
The fuel consumption (fraction of biomass pools) of each dead biomass
pool in the area affected by fire on a given day ( )
is a function of effective fuel moisture
)
is a function of effective fuel moisture  and size
class fc (Eqn B1, B4 and B5, Thonicke et al. 2010). The
fraction of each fuel class that is consumed decreases as its moisture
content relative to its moisture of extinction (
and size
class fc (Eqn B1, B4 and B5, Thonicke et al. 2010). The
fraction of each fuel class that is consumed decreases as its moisture
content relative to its moisture of extinction ( )
increases.
)
increases.

 and
and  are parameters, the value of which
is modulated by both size class
are parameters, the value of which
is modulated by both size class  and by the effective fuel
moisture class
and by the effective fuel
moisture class  , defined by
, defined by  .
.
 and
and  are defined for low-, mid-, and
high-moisture conditions, the boundaries of which are also functions of
the litter size class following Peterson and Ryan 1986 (page
802). The fuel burned,
are defined for low-, mid-, and
high-moisture conditions, the boundaries of which are also functions of
the litter size class following Peterson and Ryan 1986 (page
802). The fuel burned,  (Kg m
(Kg m day
day ) iscalculated from
) iscalculated from  for each fuel
class:
for each fuel
class:

Where 0.45 converts from carbon to biomass. The total fuel consumption,
 (Kg m
(Kg m ), used to calculate fire
intensity, is then given by
), used to calculate fire
intensity, is then given by

There is no contribution from the 1000 hour fuels to the patch-level
 used in the fire intensity calculation.
used in the fire intensity calculation.
1.18.6. Fire Intensity¶
Fire intensity at the front of the burning area ( , kW
m
, kW
m ) is a function of the total fuel consumed
(
) is a function of the total fuel consumed
( ) and the rate of spread at the front of the
fire,
) and the rate of spread at the front of the
fire,  (m min
(m min ) (Eqn 15
Thonicke et al. 2010)
) (Eqn 15
Thonicke et al. 2010)

where  is the energy content of fuel (Kj/Kg - the
same, 18000 Kj/Kg for all fuel classes). Fire intensity is used to define whether an
ignition is successful. If the fire intensity is greater than 50Kw/m
then the ignition is successful.
is the energy content of fuel (Kj/Kg - the
same, 18000 Kj/Kg for all fuel classes). Fire intensity is used to define whether an
ignition is successful. If the fire intensity is greater than 50Kw/m
then the ignition is successful.
1.18.7. Fire Duration¶
Fire duration is a function of the fire danger index with a maximum
length of  (240 minutes in
Thonicke et al. 2010 Eqn 14, derived from Canadian Forest
Fire Behaviour Predictions Systems)
(240 minutes in
Thonicke et al. 2010 Eqn 14, derived from Canadian Forest
Fire Behaviour Predictions Systems)

1.18.8. Fire Danger Index¶
Fire danger index (fdi) is a representation of the effect of
meteorological conditions on the likelihood of a fire. It is calculated
for each gridcell as a function of the Nesterov Index .
 is calculated from
is calculated from  as
as

where  = 0.00037 following
Venevsky et al. 2002.
= 0.00037 following
Venevsky et al. 2002.
1.18.9. Area Burned¶
Total area burnt is assumed to be in the shape of an ellipse, whose
major axis  (m) is determined by the forward and
backward rates of spread (
(m) is determined by the forward and
backward rates of spread ( and
and  respectively).
respectively).

 is a function of
is a function of  and windspeed (Eqn 10
Thonicke et al. 2010)
and windspeed (Eqn 10
Thonicke et al. 2010)

The minor axis to major axis ratio (i.e. the length-to-breadth ratio)  of the ellipse is
determined by the windspeed. If the windspeed (
of the ellipse is
determined by the windspeed. If the windspeed ( ) is less than
16.67 m min
) is less than
16.67 m min (i.e., 1 km hr
(i.e., 1 km hr  ) then
) then  . Otherwise (Eqn 12 and 13,
Thonicke et al. 2010, Eqn 79 and 80 Canadian
Forest Fire Behavior Prediction System Ont.Inf.Rep. ST-X-3, 1992,
as corrected in errata reported in Information Report GLC-X-10 by Bottom et al., 2009)
. Otherwise (Eqn 12 and 13,
Thonicke et al. 2010, Eqn 79 and 80 Canadian
Forest Fire Behavior Prediction System Ont.Inf.Rep. ST-X-3, 1992,
as corrected in errata reported in Information Report GLC-X-10 by Bottom et al., 2009)

 and
and  are the fractions of the patch
surface covered by grass and trees respectively.
are the fractions of the patch
surface covered by grass and trees respectively.
The total area burned ( in m
in m ) is therefore
(Eqn 11, Thonicke et al. 2010)
) is therefore
(Eqn 11, Thonicke et al. 2010)
where  is the number of fires.
is the number of fires.
1.18.10. Crown Damage¶
 is the fraction of the crown which is consumed by the
fire. This is calculated from scorch height
is the fraction of the crown which is consumed by the
fire. This is calculated from scorch height  , tree height
, tree height
 and the crown fraction parameter
and the crown fraction parameter  (Eqn 17
Thonicke et al. 2010):
(Eqn 17
Thonicke et al. 2010):

The scorch height  (m) is a function of the fire intensity,
following Byram, 1959, and is proportional to a plant
functional type specific parameter
(m) is a function of the fire intensity,
following Byram, 1959, and is proportional to a plant
functional type specific parameter  (Eqn 16
Thonicke et al. 2010):
(Eqn 16
Thonicke et al. 2010):

where  is the fraction of the above-ground
biomass in each plant functional type.
is the fraction of the above-ground
biomass in each plant functional type.
1.18.11. Cambial Damage and Kill¶
The cambial kill is a function of the fuel consumed  ,
the bark thickness
,
the bark thickness  , and
, and  , the duration of
cambial heating (minutes) (Eqn 8, Peterson and Ryan 1986):
, the duration of
cambial heating (minutes) (Eqn 8, Peterson and Ryan 1986):

Bark thickness is a linear function of tree diameter  ,
defined by PFT-specific parameters
,
defined by PFT-specific parameters  and
and
 (Eqn 21 Thonicke et al. 2010):
(Eqn 21 Thonicke et al. 2010):

The critical time for cambial kill,  (minutes) is given
as (Eqn 20 Thonicke et al. 2010):
(minutes) is given
as (Eqn 20 Thonicke et al. 2010):

The mortality rate caused by cambial heating  of trees
within the area affected by fire is a function of the ratio between
of trees
within the area affected by fire is a function of the ratio between
 and
and  (Eqn 19,
Thonicke et al. 2010):
(Eqn 19,
Thonicke et al. 2010):

Parameter Symbol |
Parameter Name |
Units |
indexed by |
|---|---|---|---|
|
Intercept of bark thickness function |
mm |
FT |
|
Slope of bark thickness function |
mm
cm |
FT |
|
Ratio of crown height to total height |
none |
FT |
|
Fuel moisture parameter |
|
fc |
|
Fuel Bulk Density |
kG
m |
fc |
|
Surface area to volume ratio |
cm
|
fc |
|
Intercept of fuel burned |
none |
|
|
Slope of fuel burned |
none |
|
|
Fuel Mineral Fraction |
||
|
Maximum Duration of Fire |
Minutes |
|
|
Energy content of fuel |
kJ/kG |
|
|
Flame height parameter |
FT |
1.19. Wood Harvest (The selective logging module)¶
Over half of all tropical forests have been cleared or logged, and almost half of standing old-growth tropical forests are designated by national forest services for timber production (Sist et al., 2015). Disturbances that result from logging are known to cause forest degradation at the same magnitude as deforestation each year in terms of both geographic extent and intensity, with widespread collateral damage to remaining trees, vegetation and soils, leading to disturbance to water, energy, and carbon cycling, as well as ecosystem integrity (Keller et al., 2004; Asner et al., 2004).
The selective logging module in FATES mimics the ecological, biophysical, and biogeochemical processes following a logging event. The module (1) specifies the timing and areal extent of a logging event; (2) calculates the fractions of trees that are damaged by direct felling, collateral damage, and infrastructure damage, and adds these size-specific plant mortality types to FATES; (3) splits the logged patch into disturbed and intact new patches; (4) applies the calculated survivorship to cohorts in the disturbed patch; and (5) transports harvested logs off-site by adding the remaining necromass from damaged trees into coarse woody debris and litter pool.
1.19.1. Logging practices¶
The logging module struture and parameterization is based on detailed field and remote sensing studies (Putz et al., 2008; Asner et al., 2004; Pereira Jr et al., 2002; Asner et al., 2005; Feldpausch et al., 2005). Logging infrastructure including roads, skids, trails, and log decks are represented (Figure 1.17.1). The construction of log decks used to store logs prior to road transport leads to large canopy openings but their contribution to landscape-level gap dynamics is small. In contrast, the canopy gaps caused by tree felling are small but their coverage is spatially extensive at the landscape scale. Variations in logging practices significantly affect the level of disturbance to tropical forest following logging (Pereira Jr et al., 2002; Macpherson et al., 2012; Dykstra, 2002; Putz et al., 2008.
Logging operations in the tropics are often carried out with little planning, and typically use heavy machinery to access the forests accompanied by construction of excessive roads and skid trails, leading to unnecessary tree fall and compaction of the soil. We refer to these typical operations as conventional logging (CL). In contrast, reduced impact logging (RIL) is a practice with extensive pre-harvest planning,where trees are inventoried and mapped out for the most efficient and cost-effective harvest and seed trees are deliberately left on site to facilitate faster recovery. Through planning, the construction of skid trails and roads, soil compaction and disturbance can be minimized. Vines connecting trees are cut and tree-fall directions are controlled to reduce damages to surrounding trees. Reduced impact logging results in consistently less disturbance to forests than conventional logging (Pereira Jr et al. 2002; Putz et al. 2008).
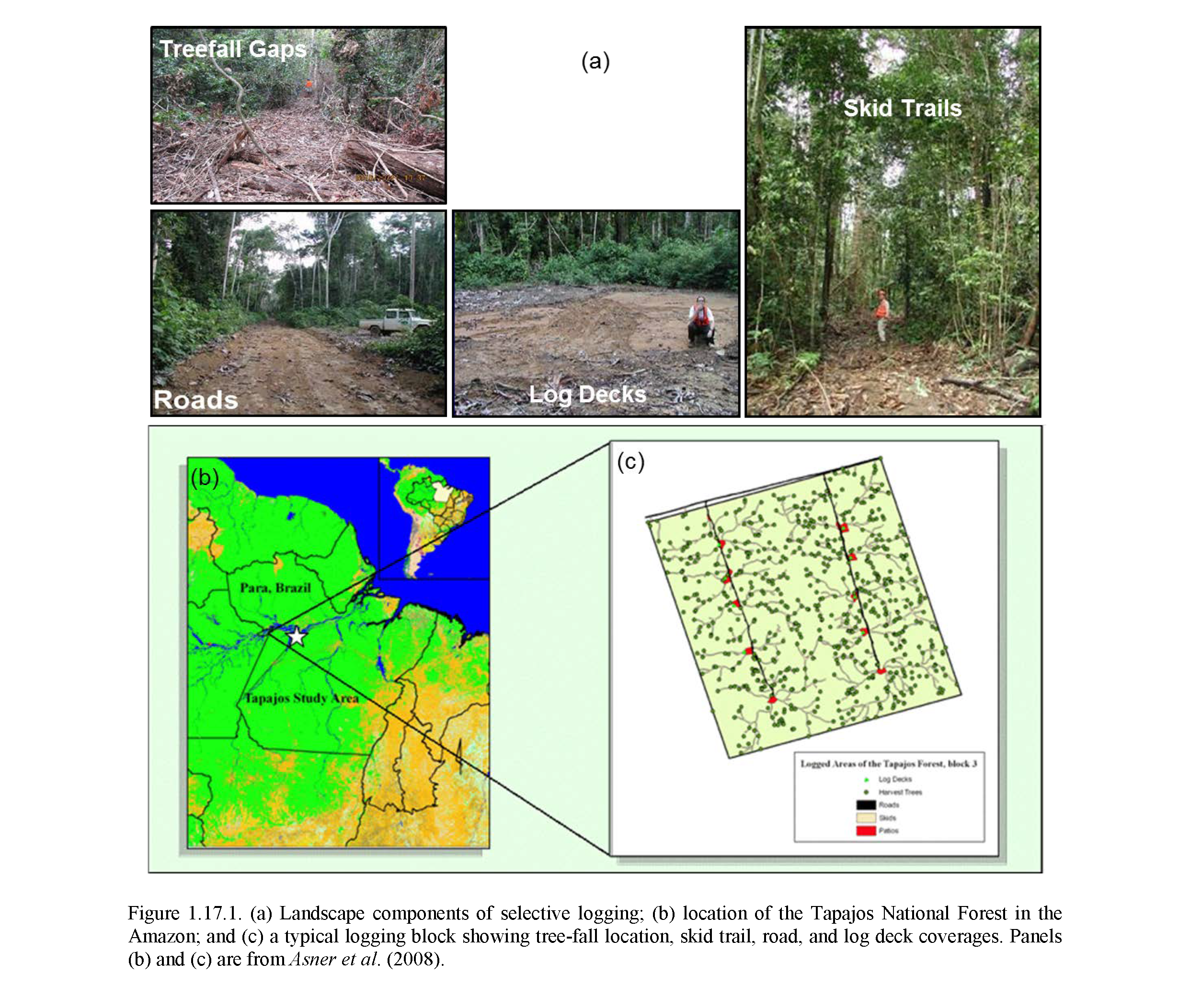
1.19.2. Mortality associated with logging¶
The FATES logging module was designed to represent a range of logging practices in field operations
at a landscape level. Once logging events are activated, we define three types of mortality
associated with logging practices: direct-felling mortality ( ),
collateral mortality (
),
collateral mortality ( ), and mechanical mortality (
), and mechanical mortality ( ).
The direct felling mortality represents the fraction of trees selected for harvesting that are greater
or equal to a diameter threshold (this threshold is defined by the diameter at breast height (DBH) = 1.3 m
denoted as
).
The direct felling mortality represents the fraction of trees selected for harvesting that are greater
or equal to a diameter threshold (this threshold is defined by the diameter at breast height (DBH) = 1.3 m
denoted as  ); collateral mortality denotes the fraction of adjacent trees
that killed by felling of the harvested trees; and the mechanical mortality represents the
fraction of trees killed by construction of log decks, skid trails and roads for accessing
the harvested trees, as well as storing and transporting logs offsite (Figure 1.17.1a).
In a logging operation, the loggers typically avoid large trees when they build log decks, skids,
and trails by knocking down relatively small trees as it is not economical to knock down large trees.
Therefore, we implemented another DBH threshold,
); collateral mortality denotes the fraction of adjacent trees
that killed by felling of the harvested trees; and the mechanical mortality represents the
fraction of trees killed by construction of log decks, skid trails and roads for accessing
the harvested trees, as well as storing and transporting logs offsite (Figure 1.17.1a).
In a logging operation, the loggers typically avoid large trees when they build log decks, skids,
and trails by knocking down relatively small trees as it is not economical to knock down large trees.
Therefore, we implemented another DBH threshold,  , so that only a fraction
of trees
, so that only a fraction
of trees  (called mechanical damage fraction) are removed for
building infrastructure (Feldpausch et al., 2005).
(called mechanical damage fraction) are removed for
building infrastructure (Feldpausch et al., 2005).
1.19.3. Patch dynamics following logging disturbance¶
To capture the disturbance mechanisms and degree of damage associated with logging practices
at the landscape level, we apply the mortality types following a workflow designed to correspond to
field operations. In FATES, as illustrated in Figure 1.17.2., individual trees of all plant functional types (PFTs)
in one patch are grouped into cohorts of similar-sized trees, whose size and population sizes evolve in time
through processes of recruitment, growth, and mortality. As described
abve, cohorts are organized into canopy and understory layers,
which are subject to different light conditions (Figure 1.17.2a). When logging activities occur,
the canopy trees and a portion of big understory trees lose their crown coverage through direct felling
for harvesting logs, or as a result of collateral and mechanical damages ((Figure 1.17.2b). The fractions of
(only the) canopy trees affected by the three mortality mechanisms are then summed up to specify the areal
percentages of an old (undisturbed) and a new (disturbed) patch caused by logging in the patch fission process
(Figure 1.17.2c). After patch fission, the canopy layer over the disturbed patch is removed,
while that over the undisturbed patch stays untouched (Figure 1.17.2d). In the undisturbed patch, the survivorship of
understory trees is calculated using an understory death fraction consistent with whose default value corresponds
to that used for natural disturbance ( , 0.559). To differentiate logging from natural disturbance,
a slightly elevated, logging-specific understory death fraction is applied in the disturbed patch instead at the
time of the logging event. Based on data from field surveys over logged forest plots in southern Amazon
(Feldpausch et al., 2005), understory death fraction corresponding to logging
is now set to be 0.65 as the default, but can be modified via the FATES parameter file (Figure 1.17.2e).
Therefore, the logging operations will change the forest from the undisturbed state shown in Figure 1.17.2a
to a disturbed state in Figure 1.17.2f in the logging module. It is worth mentioning that the newly generated
patches are tracked according to age since disturbance and will be merged with other patches of similar
canopy structure following the patch fusion processes in FATES in later time steps of a simulation,
pending the inclusion of separate land-use fractions for managed and unmanaged forest.
, 0.559). To differentiate logging from natural disturbance,
a slightly elevated, logging-specific understory death fraction is applied in the disturbed patch instead at the
time of the logging event. Based on data from field surveys over logged forest plots in southern Amazon
(Feldpausch et al., 2005), understory death fraction corresponding to logging
is now set to be 0.65 as the default, but can be modified via the FATES parameter file (Figure 1.17.2e).
Therefore, the logging operations will change the forest from the undisturbed state shown in Figure 1.17.2a
to a disturbed state in Figure 1.17.2f in the logging module. It is worth mentioning that the newly generated
patches are tracked according to age since disturbance and will be merged with other patches of similar
canopy structure following the patch fusion processes in FATES in later time steps of a simulation,
pending the inclusion of separate land-use fractions for managed and unmanaged forest.
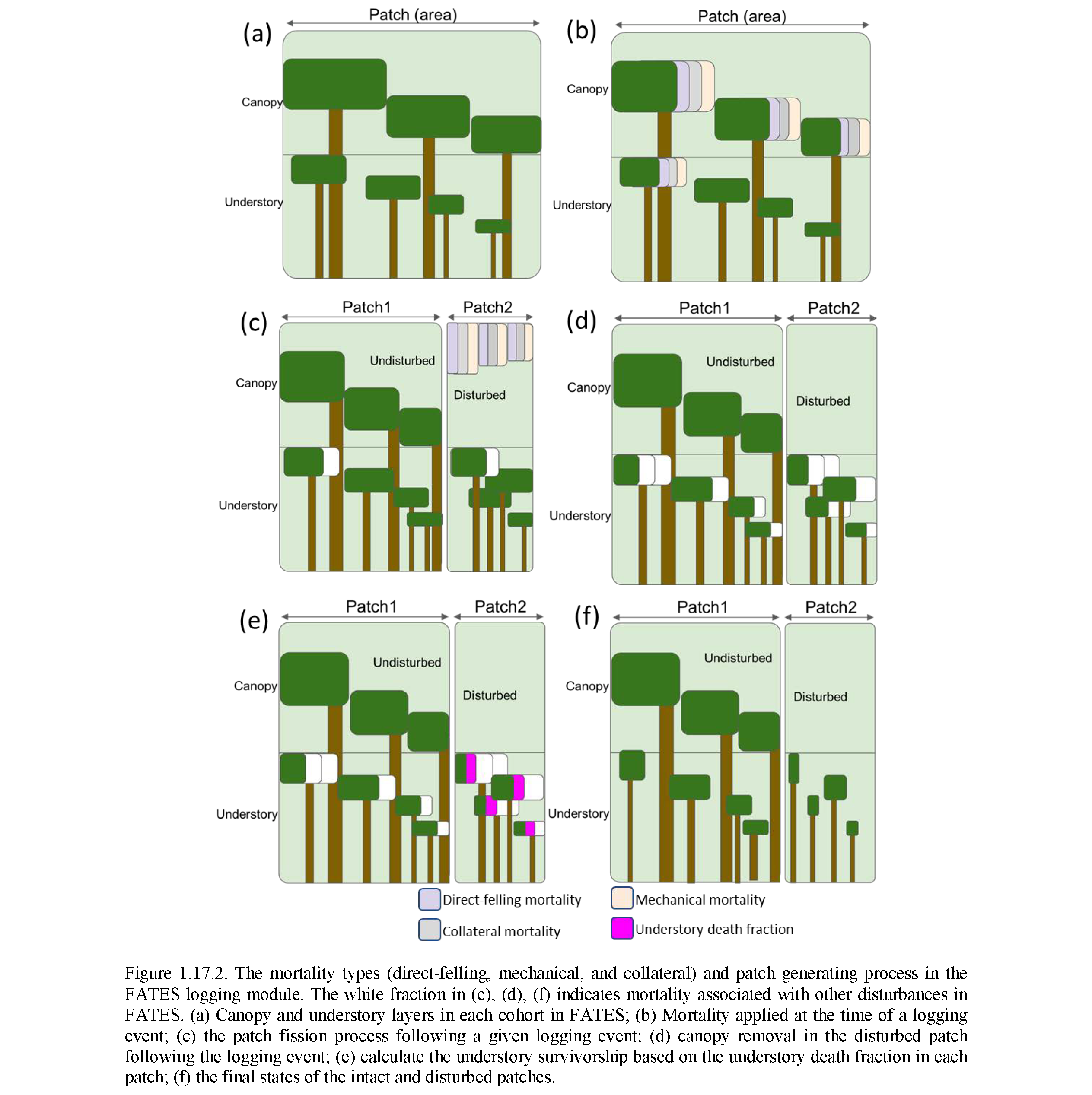
1.19.4. Flow of necromass following logging disturbance¶
Logging operations affect forest structure and composition, and also carbon cycling (Palace et al., 2008) by modifying the live biomass pools and flow of necromass (Figure 1.17.3). Following a logging event, the logged trunk products from the harvested trees are transported off-site (as an added carbon pool for resource management in the model), while their branches enter the coarse woody debris (CWD) pool, and their leaves and fine roots enter the litter pool. Similarly, trunks and branches of the dead trees caused by collateral and mechanical damages also become CWD, while their leaves and fine roots become litter. Specifically, the densities of dead trees as a result of direct felling, collateral, and mechanical damages in a cohort are calculated as follows:



where  stands for the area of the patch being logged, and
stands for the area of the patch being logged, and  is the number of individuals
in the cohort where the mortality types apply (i.e., as specified by the size thresholds,
is the number of individuals
in the cohort where the mortality types apply (i.e., as specified by the size thresholds,  and
and  ). For each cohort, we denote
). For each cohort, we denote  and
and  , respectively.
, respectively.
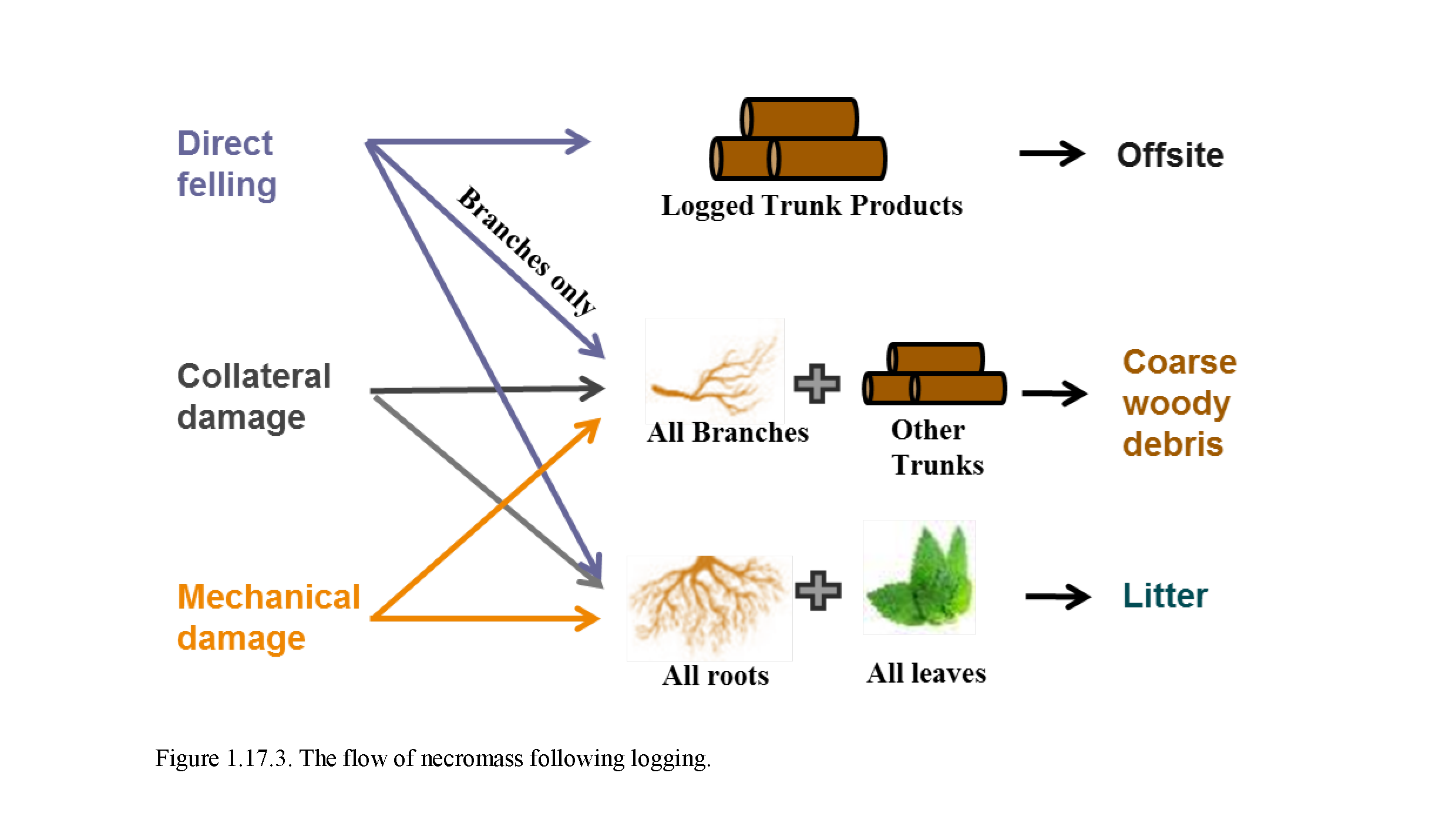
Leaf litter (![Litter_{leaf}, [kg C]](_images/math/1a0ac5a23c9f9cb304cefd6af85535a7a7f0d232.png) ) and root litter (
) and root litter (![Litter_{root}, [kg C]](_images/math/b6bbd8f6144d2166e1b2adeced11129f0f5c4542.png) ) at the cohort level
are then calculated as:
) at the cohort level
are then calculated as:
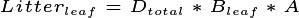

where  ,
,  ,
,  are live biomass in leaves and fine roots, and stored
biomass in the labile carbon reserve in all individual trees in the cohort of interest.
are live biomass in leaves and fine roots, and stored
biomass in the labile carbon reserve in all individual trees in the cohort of interest.
Following the existing CWD structure in FATES (Fisher et al., 2015), CWD in the logging module
is first separated into two categories: above-ground CWD and below-ground CWD. Within each category, four size classes
are tracked based on their source, following Thonicke et al. (2010): trunks, large branches,
small branches and twigs. Above-ground CWD from trunks (![CWD_{trunk_{agb}}, [kg C]](_images/math/00d9792e3889d79b90602afc0f40cd907b0889fe.png) ) and large branches/small
branches/twig (
) and large branches/small
branches/twig (![CWD_{branch_{agb}}, [kg C]](_images/math/1ae29013000f8380307d84261db218afa3206eab.png) ) are calculated as follows:
) are calculated as follows:


where  is the amount of above ground stem biomass in the cohort,
is the amount of above ground stem biomass in the cohort,  and
and  represent the fraction of trunks and large branches/small branches/twig. Similarly, the below-ground CWD from
trunks (
represent the fraction of trunks and large branches/small branches/twig. Similarly, the below-ground CWD from
trunks (![CWD_{trunk_{bg}}, [kg C]](_images/math/c2c7ace5a6f6882fe4a4c7094787856d9c486c12.png) ) and branches/twig (
) and branches/twig (![CWD_{branch_{bg}}, [kg C]](_images/math/a2f21fce9996690bd1736cc69fb3f9a650f1996d.png) ) are calculated as follows:
) are calculated as follows:

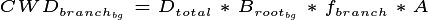
where ![B_{croot} [kg C]](_images/math/922333eb0259dff902b735bcd70b9c93a8bec476.png) is the amount of coarse root biomass in the cohort. Site-level total litter and CWD inputs
can then be obtained by integrating the corresponding pools over all the cohorts in the site. To ensure mass conservation,
is the amount of coarse root biomass in the cohort. Site-level total litter and CWD inputs
can then be obtained by integrating the corresponding pools over all the cohorts in the site. To ensure mass conservation,

where  is total loss of biomass due to logging,
is total loss of biomass due to logging,  and
and  are the
increments in litter and CWD pools, and
are the
increments in litter and CWD pools, and  represents harvested logs shipped offsite.
represents harvested logs shipped offsite.
Following the logging event, the forest structure and composition in terms of cohort distributions, as well as the live biomass and necromass pools are updated. Following this logging event update to forest structure, the native processes simulating physiology, growth and competition for resources in and between cohorts resume. Since the canopy layer is removed in the disturbed patch, the existing understory trees are promoted to the canopy layer, but, in general, the canopy is incompletely filled in by these newly-promoted trees, and thus the canopy does not fully close. Therefore, more light can penetrate and reach the understory layer in the disturbed patch, leading to increases in light-demanding species in the early stage of regeneration, followed by a succession process in which shade tolerant species dominate gradually.
The above describes the case where the canopy is closed (by treees) prior to logging. If this is not the case, some amount of non-tree-occupied canopy area is also moved to the newly-disturbed patch so as to maintain the composition of the undisturbed patch or patches in their original state (albeit in covering a smaller area).
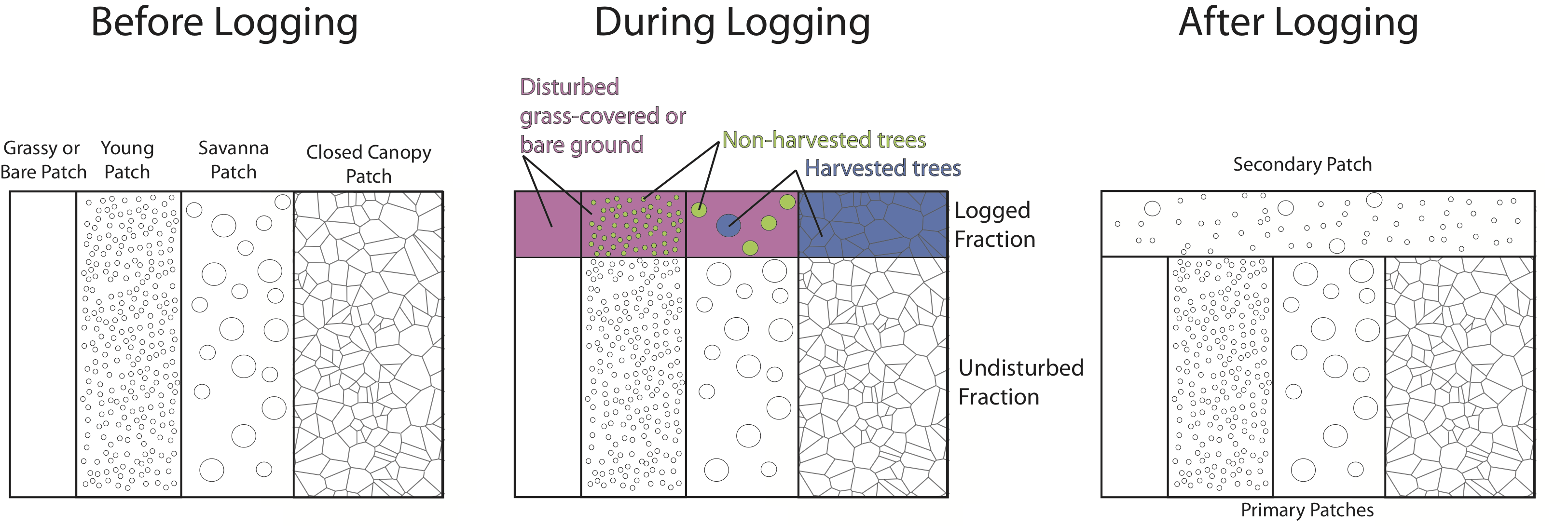
After logging occurs, the patches that have been disturbed are tracked as belonging to secondary lands, and are not fused with patches on primary lands. This allows primary and secondary land areas to be tracked, with possibly different ecological dynamics occuring on each.
1.20. Plant Hydraulic module¶
For each plant cohort, the hydraulic module tracks water flow along a soil–plant–atmosphere continuum of a representative individual tree based on hydraulic laws, and updates the water content and potential of leaves, stem, and roots with a 30 minutes model time step. Water flow from each soil layer within the root zone into the plant root system is calculated as a function of the hydraulic conductance as determined by root biomass and root traits such as specific root length, and the difference in water potential between the absorbing roots and the rhizosphere. The root distribution is based on Zeng’s (2001) two parameter power law function which takes into account the regolith depth:

where  is the fraction of fine or coarse roots in the
is the fraction of fine or coarse roots in the 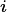 th soil
layer,
th soil
layer,  and
and 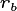 are the two parameters that determine the
vertical root distribution,
are the two parameters that determine the
vertical root distribution,  is the depth of the lower boundary
of the
is the depth of the lower boundary
of the 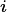 th soil layer, and
th soil layer, and  is the depth of the upper
boundary of the
is the depth of the upper
boundary of the 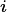 th soil layer, and
th soil layer, and  is the total regolith depth.
The vertical root distribution affects water uptake by the hydrodynamic
model by distributing the total amount of root, and thus root
resistance, through the soils.
is the total regolith depth.
The vertical root distribution affects water uptake by the hydrodynamic
model by distributing the total amount of root, and thus root
resistance, through the soils.
The total transpiration of a tree is the product of total leaf area (LA)
and the transpiration rate per unit leaf area  . In this version of
FATES-Hydro, we adopt the model developed by Vesala et al. (2017) to
take into account the effect of leaf water potential on the within-leaf
relative humidity and transpiration rate:
. In this version of
FATES-Hydro, we adopt the model developed by Vesala et al. (2017) to
take into account the effect of leaf water potential on the within-leaf
relative humidity and transpiration rate:



Where,  is the total transpiration of a tree,
is the total transpiration of a tree,  [m2] is the total leaf area,
[m2] is the total leaf area,  [kg/s/m2] is the transpiration per unit leaf area,
[kg/s/m2] is the transpiration per unit leaf area,  [kg/m3] is the density of atmospheric air,
[kg/m3] is the density of atmospheric air,  [kg/kg] is the within-leaf specific humidity,
[kg/kg] is the within-leaf specific humidity,
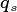 [kg/kg] is the atmosphere specific humidity,
[kg/kg] is the atmosphere specific humidity,  [m/s] is the
stoma conductance per unit leaf area,
[m/s] is the
stoma conductance per unit leaf area, 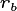 [s/m] is the leaf boundary
layer resistance,
[s/m] is the leaf boundary
layer resistance,  is a unitless scaling coefficient, which can vary between 1 and 7, and here we use a value of
3;
is a unitless scaling coefficient, which can vary between 1 and 7, and here we use a value of
3;  [Mpa] is the leaf water potential,
[Mpa] is the leaf water potential,  [1.8e-6 m3/mol] is the constant molar volume,
[1.8e-6 m3/mol] is the constant molar volume, 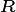 is the
universal gas constant, and
is the
universal gas constant, and  [K] is the leaf temperature.
[K] is the leaf temperature.
The sap flow from absorbing roots to the canopy through each compartment of the tree along the flow path way (absorbing roots, transport roots, stem, and leaf) is computed according to Darcy’s law in terms of the plant sapwood water conductance, the water potential gradient:

where  is the density of water;
is the density of water; 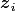 [m] is the height of the
compartment;
[m] is the height of the
compartment;  [m] is the height of the next compartment down the
flow path;
[m] is the height of the next compartment down the
flow path;  [MPa] is the water potential of the
compartment;
[MPa] is the water potential of the
compartment; 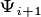 [MPa] is the water potential of the next
compartment down the flow path; and
[MPa] is the water potential of the next
compartment down the flow path; and  [kg/MPa/m/s] is the hydraulic
conductance of the compartment . The hydraulic conductance
of the compartments is by the water potential and maximum hydraulic
conductance of the compartment through the pressure-volume (P-V) curve
and the vulnerability curve (Manzoni et al. 2013, Christoffersen et al.
2016).
[kg/MPa/m/s] is the hydraulic
conductance of the compartment . The hydraulic conductance
of the compartments is by the water potential and maximum hydraulic
conductance of the compartment through the pressure-volume (P-V) curve
and the vulnerability curve (Manzoni et al. 2013, Christoffersen et al.
2016).
The plant hydrodynamic representation and numerical solver scheme within FATES-HYDRO follows Christoffersen et al. (2016). A few modifications are made to accommodate the multi-soil layers and improve the numerical stability. First, to accommodate the multi-soil layers, we have sequentially solved the Richards’ equation for each individual soil layers, with each layer-specific solution proportional to each layer’s contribution to the total root-soil conductance. Second, to improve the numerical stability, we have linearly interpolated the PV curve beyond the residual and saturated tissue water content to avoid the rare cases of overshooting in the numerical scheme under very dry or wet conditions. Third, Christoffersen et al. (2016) used three phases to describe the PV curves: 1) dehydration phases representing capillary water (sapwood only), 2) elastic cell drainage (positive turgor), and 3) continued drainage after cells have lost turgor. Due to the discontinuity of the curve between these three phases, it leads to some numerical instability. To resolve this instability, FATES-HYDRO added the Van Genuchten model (Van Genuchten 1980, July and Horton 2004) and the Campbell model (Campbell 1974) as an alternatives to describe the PV curves.
The Van Genuchten model has two advantages: 1) it is simple, with only three parameters needed for both curves, and 2) it is mechanistically based, with both the P-V curve and vulnerability curve derived from a pipe model thus are connected through the three shared parameters:


where  [MPa] is the water potential of the media (xylem in this
case);
[MPa] is the water potential of the media (xylem in this
case); ![FMC [K/K_{max}]](_images/math/589351bcdae7cd615647c4a0f8250c21ad6844f7.png) is the fraction of xylem conductivity;
is the fraction of xylem conductivity;  [/MPa] is a scaling parameter for air
entering point,
[/MPa] is a scaling parameter for air
entering point,  is the dimensionless
standardized relative water content as:
is the dimensionless
standardized relative water content as:

where  ,
, 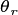 and
and  [m3/m3] are volumetric water content, residual volumetric water content, and saturated
volumetric water content correspondingly; and
[m3/m3] are volumetric water content, residual volumetric water content, and saturated
volumetric water content correspondingly; and  and
and  are
dimensionless (xylem conduits) size distribution parameters.
are
dimensionless (xylem conduits) size distribution parameters.
The stomatal conductance is modelled in the form of Ball-Berry conductance model (Ball et al. 1987, Oleson et al. 2013, Fisher et al. 2015):

where  and
and  are parameters equivalent to slope and intercept in
the Ball-Berry model correspondingly. These terms are plant strategy
dependent and can vary widely with plant functional types (Medlyn et al.
2011). The parameter
are parameters equivalent to slope and intercept in
the Ball-Berry model correspondingly. These terms are plant strategy
dependent and can vary widely with plant functional types (Medlyn et al.
2011). The parameter  is also scaled by the water stress index
is also scaled by the water stress index 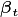 .
.
 [umol CO2/m2/s] is the net carbon assimilation rate based on Farquhar’s (1980) formula. This term
is also constrained by water stress index
[umol CO2/m2/s] is the net carbon assimilation rate based on Farquhar’s (1980) formula. This term
is also constrained by water stress index 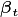 in the way that the
in the way that the  is scaled by
is scaled by 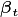 as
as 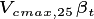 (Fisher et al. 2018).
(Fisher et al. 2018).  [Pa] is the CO2 partial pressure at the
leaf surface,
[Pa] is the CO2 partial pressure at the
leaf surface,  [Pa] is the vapor pressure at the leaf surface,
[Pa] is the vapor pressure at the leaf surface,  [Pa] is the saturation vapor pressure inside the leaf at a
given vegetation temperature when
[Pa] is the saturation vapor pressure inside the leaf at a
given vegetation temperature when  .
.
The water stress index, a proxy for stomatal closure in response to desiccation, is determined by the leaf water potential adopted from the FMCgs term from Christoffersen et al. (2016):

where 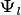 [MPa] is the leaf water potential,
[MPa] is the leaf water potential,  [MPa] is the leaf
water potential of 50% stomatal closure, and
[MPa] is the leaf
water potential of 50% stomatal closure, and  governs the
steepness of the function. For a given set of
governs the
steepness of the function. For a given set of  , the
, the  controls the degree of hydraulic vulnerability segmentation
(Christoffersen et al. 2016, Powell et al. 2017). A more negative
controls the degree of hydraulic vulnerability segmentation
(Christoffersen et al. 2016, Powell et al. 2017). A more negative
 means that, during leaf dry down from full turgor, the
stomatal aperture stays open and thus allows the transpiration rate to
remain high and xylem to dry out, which thus can maintain high
photosynthetic rates at the risk of exposing xylem to embolism and thus
plant mortality. Conversely, a plant with a less negative
means that, during leaf dry down from full turgor, the
stomatal aperture stays open and thus allows the transpiration rate to
remain high and xylem to dry out, which thus can maintain high
photosynthetic rates at the risk of exposing xylem to embolism and thus
plant mortality. Conversely, a plant with a less negative  will
close stomata quickly during leaf dry down, thus limiting transpiration
and the risk of xylem embolism and mortality associated with it.
will
close stomata quickly during leaf dry down, thus limiting transpiration
and the risk of xylem embolism and mortality associated with it.
References
Ball, J. Timothy, Ian E. Woodrow, and Joseph A. Berry. 1987. “A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions.” Progress in photosynthesis research. Springer, Dordrecht, 221-224.
Campbell, G.S., 1974. A simple method for determining unsaturated conductivity from moisture retention data. Soil science, 117(6), pp.311-314.
Christoffersen, Bradley O et al. 2016. “Linking Hydraulic Traits to Tropical Forest Function in a Size-Structured and Trait-Driven Model (TFS v . 1-Hydro ).” : 4227–55.
Fisher, R. a. et al. 2015. “Taking off the Training Wheels: The Properties of a Dynamic Vegetation Model without Climate Envelopes, CLM4.5(ED).” Geoscientific Model Development 8(11): 3593–3619.
Jury, W.A. and Horton, R., 2004. Soil physics. John Wiley & Sons.
Manzoni, S., 2014. Integrating plant hydraulics and gas exchange along the drought-response trait spectrum. Tree physiology, 34(10), pp.1031-1034.
Oleson, Keith W et al. 2013. “Technical Description of Version 4.5 of the Community Land Model (CLM) Coordinating.” In Natl. Cent. Atmos. Res. Tech. Note, Natl. Cent. for Atmos. Res., Boulder, Colo.
Van Genuchten, M.T., 1980. A closed‐form equation for predicting the hydraulic conductivity of unsaturated soils. Soil science society of America journal, 44(5), pp.892-898.
Vesala, T., Sevanto, S., Gronholm, T., Salmon, Y., Nikinmaa, E., Hari, P., & Holtta, T. 2017. “Effect of leaf water potential on internal humidity and CO2 dissolution: Reverse transpiration and improved water use efficiency under negative pressure.” Frontiers in Plant Science, 8, 54.
Zeng, Xubin. 2001. “Global Vegetation Root Distribution for Land Modeling.” Journal of Hydrometeorology 2(5): 525–30.
1.21. Crown Damage Module¶
The crown damage module represents crown damage as a reduction in crown area and the biomass of tissues in the crown (leaves, sapwood, storage, structural and reproductive tissues), implemented via changes to allometric relationships. Damage currently does not change the height of cohorts or the biomass of the stem.
We treat damage as a categorical variable with each cohort associated with a ‘damage class’ that describes its degree of crown loss.
Damage classes can be set in the parameter file via damage_bin_edges, which sets the lower bin edges for the percentage of crown loss
in each damage class. Damage classes do not need to be evenly spaced. Damage class is an argument to allometric equations and
is used to reduce the biomass of crown tissues. For example:

where  is leaf biomass.
is leaf biomass.
We reduce sapwood and structural tissues in proportion to their branch fraction.

where  is sapwood biomass,
is sapwood biomass, 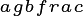 is aboveground biomass fraction and
is aboveground biomass fraction and 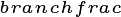 is the branch fraction.
Branch fraction is calculated as the sum of the first three coarse woody debris pools (i.e. excluding the main stem).
is the branch fraction.
Branch fraction is calculated as the sum of the first three coarse woody debris pools (i.e. excluding the main stem).
Damage is not currently linked to explicit drivers. The timing of damage events is set by the damage_event_code parameter - described in table
Crown damage event codes.
Event code |
Description |
|---|---|
1 |
Damage is off |
2 |
Damage occurs on the first time step |
3 |
Damage occurs every day (not recommended) |
4 |
Damage occurs once a month (on the first day) |
negative number |
Damage occurs annually on the specified day of the year |
YYYYMMDD |
Damage occurs on a given date. |
The damage_frac parameter determines the proportion of a cohort that is damaged with each damage event.
Part of the cohort keeps its current damage class, while the damaged portion of the cohort is equally divided into
cohorts with higher damage classes. In the figure below there are five damage classes including undamaged and
damage_frac is set to 0.1. Of the intial cohort of 1000 individuals
25 individuals are therefore moved into each of the four higher damage classes.
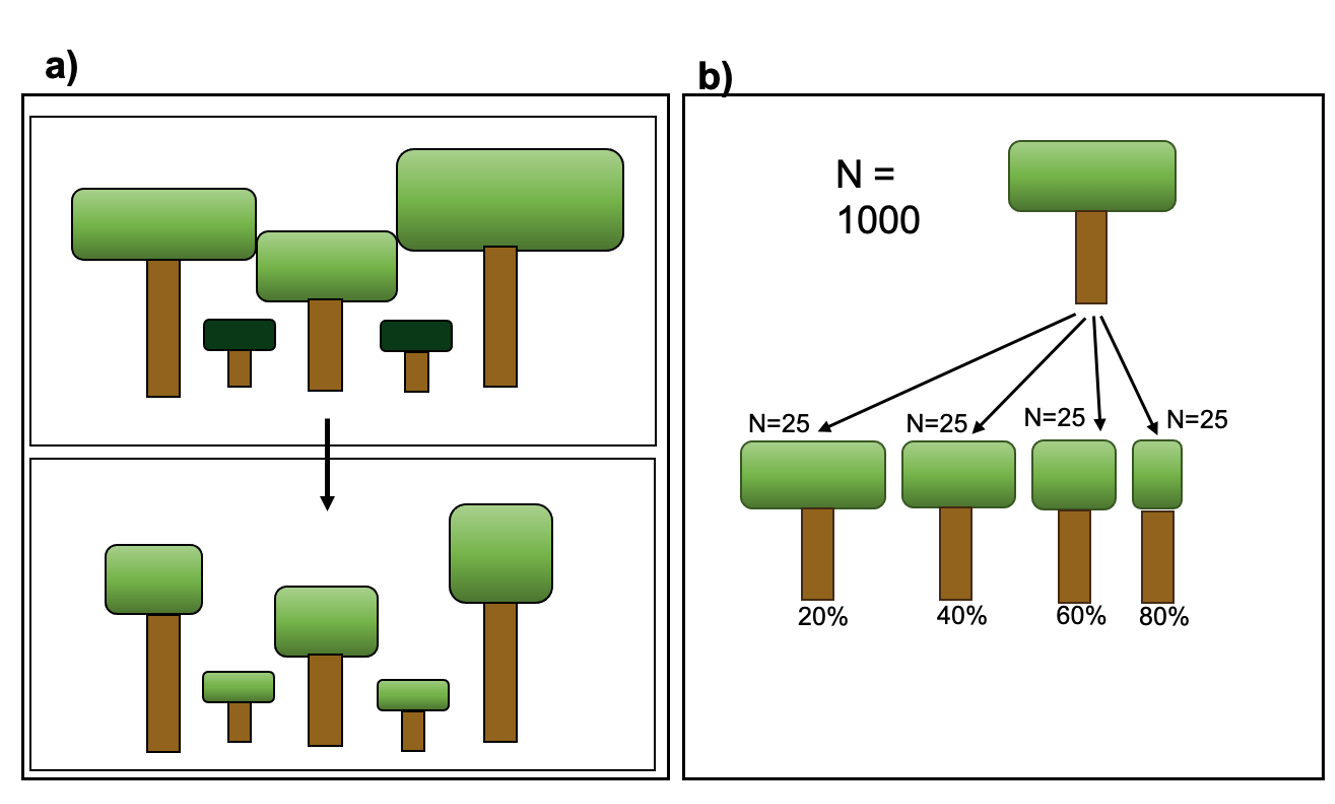
Recovery from crown damage is set via the damage_recovery_scalar parameter. A value of zero means that during daily
allocation of NPP, no recovery occurs and damaged cohorts will allocate all available carbon to growth along their
altered allometric trajectories. A value of one means that cohorts will use all available carbon to regrow damaged tissues,
at the expense of dbh growth. The maximum number of individuals of a cohort that can recover in each timestep ( ) is
a function of the available allocatable carbon to grow with (
) is
a function of the available allocatable carbon to grow with ( ) and the change in carbon between
the damage class
) and the change in carbon between
the damage class 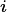 and
and  (
( ):
):
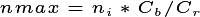
Where  is the initial number density of the cohort. The number of plants that recover is
then
is the initial number density of the cohort. The number of plants that recover is
then 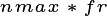 where
where  is the
is the damage_recovery_scalar parameter.
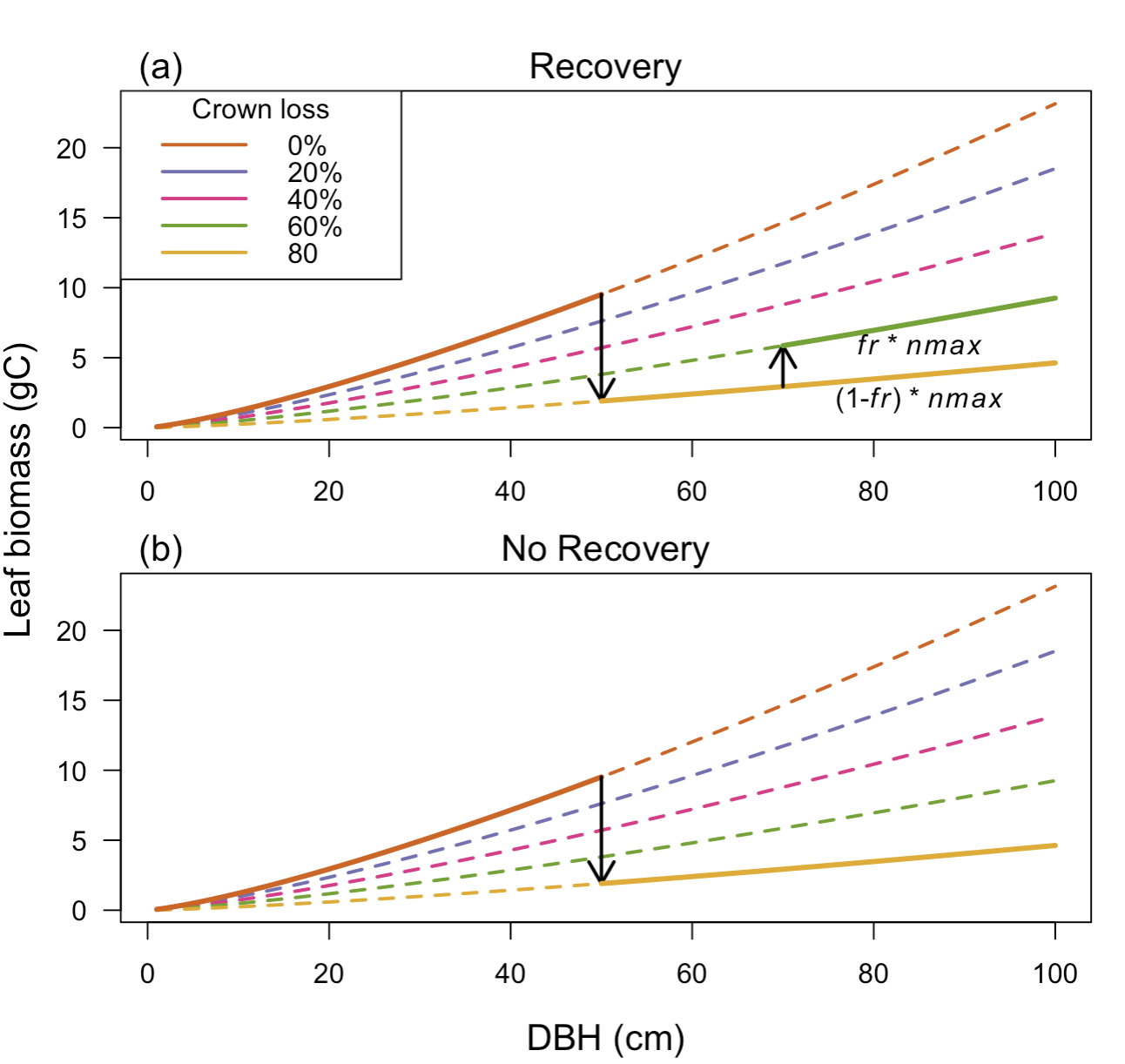
Crown damage in FATES can lead to mortality via carbon starvation. However, to capture mortality associated with crown loss
from mechanisms not currently in FATES (e.g. pathogen entry) an additional mortality term describes an increase
in mortality with crown loss  .
.

where  is the fraction of crown loss,
is the fraction of crown loss,  is the rate that mortality increases with crown loss,
and
is the rate that mortality increases with crown loss,
and  is the inflection point of the curve, i.e. the crown loss at which annual mortality rate has increased to 50%.
is the inflection point of the curve, i.e. the crown loss at which annual mortality rate has increased to 50%.
For an application of the FATES crown damage module see Needham et al. (2022).
1.22. FATES Reduced Complexity Configurations¶
The full FATES model has a high degree of structural complexity, with interactions between processes acting at short timescales such as photosynthesis and processes acting at longer timescales such as competition and community restructuring. In order to better isolate different processes, allow for cleaner experimental design, and facilitate calibration and testing of different model components, FATES includes a number of reduced-complexity configurations. A summary of these configurations is shown in table FATES reduced-complexity modes.
Mode |
How to enable |
Vegetation structure |
Leaf Area Index |
Photosynthesis and Physiology |
Competition between PFTs for canopy space |
|---|---|---|---|---|---|
Primarily site-level modes |
|||||
Static Stand Structure (ST3) |
|
Fixed after initialization |
Fixed after initialization |
Active |
No |
Prescribed Physiology |
|
Active |
Inactive |
Prescribed NPP per unit crown area and mortality rate |
Active if multiple PFTs present |
Primarily large-scale modes |
|||||
Satellite Phenology mode (FATES-SP) |
|
Simplified: 1 patch per PFT and one cohort per patch |
Prescribed via dynamic dataset |
Active |
No |
No competition mode, with prescribed biogeography (FATES-nocomp) |
|
Active |
Active |
Active |
No competition: Each PFT allotted a total fixed areas based on input dataset |
No competition mode, without prescribed biogeography |
|
Active |
Active |
Active |
No competition: Each PFT allotted the same area everywhere |
Prescribed biogeography |
|
Active |
Active |
Active |
Active, put PFTs only allowed to grow where they are present in input dataset |
Full FATES |
Active |
Active |
Active |
Active |
Each of these modes is described in more detail below. We here separate them into those that are primarily intended for site-scale simulations and those that are primarily intended for large-scale simulations; However we note that all modes have valid use-cases for both site-scale and large-scale simulations.
1.22.1. Primarily site-level FATES reduced complexity modes¶
Two reduced complexity configurations are designed primarily for site-level testing. These are Static Stand Structure mode and Prescribed Physiology mode, which enable only the fast-timesale and slow-timescale processes, respectively.
1.22.1.1. Static Stand Structure Mode¶
This mode turns of all growth and mortality processes. It is best used with an inventory initialization to set the initial stand structure as has been observed at a given location. By turning off growth and mortality, this mode cuts all feedbacks between fast and slow processes, and thus can be used to look at changes to physiological processes or parameters conditional on a given ecosystem structure, or alternately can be used to calibrate physiological dynamics at a specific site given known ecosystem structure. Note that leaf phenology is also disabled in this mode, and thus a user may want to accomplish similar goals using the Satellite Phenology mode for sites with strong phenological cycles.
1.22.1.2. Prescribed Physiology Mode¶
This mode ignores all prognositc physiology calculatino,and instead allows the user to assert growth and mortality rates in the canopy and understory. Growth rates are specified via a parameter that governs the NPP per unit crown area. The crown area scaling is to align overall growth trajectories as plants grow in size with the full FATES model: since both light interception and maintenance respiration (assuming the leaf biomass allometric exponent is the same as that for crown area) scale with leaf and crown area, this implies an NPP scaling with crown area as well. Thus this mode allows testign the effects of different ways of organizing the canopy, or other slow-timescale processes, conditional on some known growth and mortality rates.
1.22.2. Primarily large-scale FATES reduced complexity modes¶
The primarily large-scale reduced complexity modes are designed to allow separation of processes in support of model complexity hierarchies and global calibration efforts. A schematic of these configurations is below:
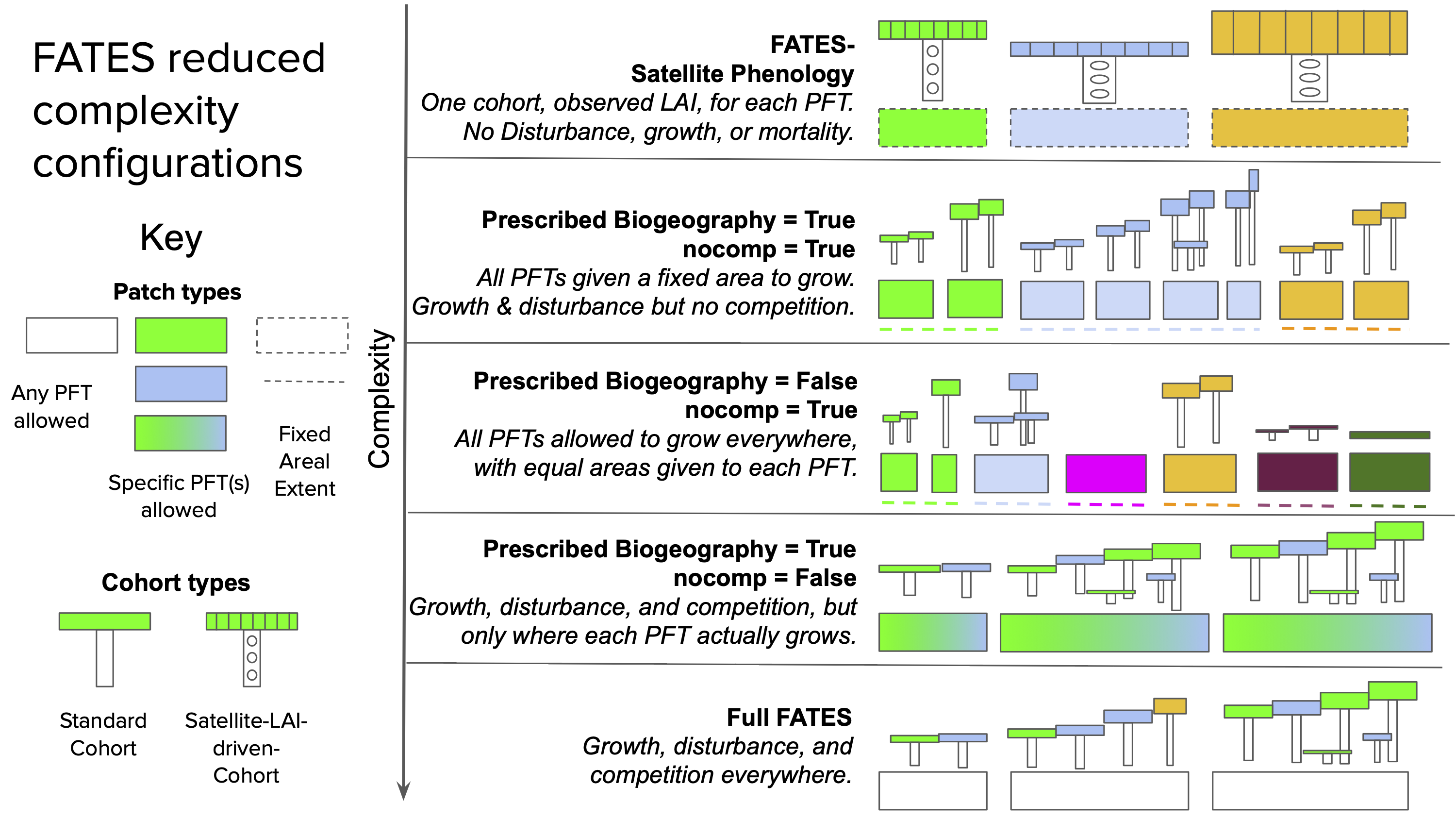
1.22.2.1. Satellite Phenology (FATES-SP) Mode¶
THi sis the simples of the large-scale configurations, and reverts the behavior of the model as close as possible to the existing CLM-SP and ELM-SP configurations. In this mode, FATES is given information about the static areal coverage of each PFT, as well as time-varying information about LAI and canopy height in the model. FATES uses this information to construct a canopy structure with a single patch per PFT and a single cohort per patch, whose stem diameter corresponds allometrically to the canopy height, and whose number density allows the cohort to fill the patch given the allometric crown area per plant. Leaf biomass is dynamically calculated to achieve the specified LAI for each PFT.
1.22.2.2. No competition with prescribed biogeography (nocomp) mode¶
In this mode, all processes are active except for light competition between PFTs. Each PFT is given a total patch area to grow on, but unlike FATES-SP mode, disturbance can occur on each patch and thus the space allocated to each PFT may be split into one or more patches based on disturbance history. Each patch has a PFT label, and only that PFT is allowed to grow on the patch. Cohorts of agiven PFT compete against each other for canopy access and thus light.
1.22.2.3. No competition without prescribed biogeography mode¶
This mode is imilar to the ‘nocomp’ mode described above, but instead of each PFT being allocated areas based on a PFT map read from an input surface dataset, each PFT is allocated the same area on all gridcells. Thus it can be used for specific experiemnts looking at PFT differences across climate gradients.
In no competition with and without prescribed biogeography cohorts can be initialised based on a given dbh, rather than spun up from bare ground, by setting the fates_recruit_init_density parameter to a negative number, which is then interpreted as initial dbh.
1.22.2.4. Prescribed biogeography with competition mode¶
In this mode, PFTs compete against each other, but a given PFT is only allowed to grow and exist in places where it has some coverage in an input surface datset. Thus, for example, boreal plants are not allowed to grow in the tropics and vice-versa, but competition betwen various plants that coexist in the surface datset can occur. This mode may also be used to impose biogeographic differences between, e.g. neotropical versus African and/or Asian tropical forest PFTs.
1.22.2.5. Full FATES¶
All processes are active.












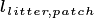



















 )
)








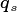












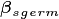

 devoted to
reproduction
devoted to
reproduction![\delta RA
[\delta dbh]^{-1}](_images/math/05d76629cd399ad168605fc682d322194df4bf38.png)
 (fates_trs_seed_decay_rate)
(fates_trs_seed_decay_rate) (fates_trs_seedling_root_depth)
(fates_trs_seedling_root_depth) (fates_trs_seedling_h2o_mort_a)
(fates_trs_seedling_h2o_mort_a) (fates_trs_seedling_h2o_mort_b)
(fates_trs_seedling_h2o_mort_b) (fates_trs_seedling_h2o_mort_c)
(fates_trs_seedling_h2o_mort_c)
 (fates_trs_recruit_hgt_min)
(fates_trs_recruit_hgt_min)








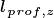








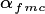
 C
C