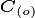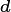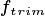1.5.2.2.2. Allocation Hypothesis 2: Allometrically Guided, Carbon and Nutrients with Prioritization and Flexible Target Stoichiometry¶

This hypothesis assumes there is a single carbon species, and an arbitrary number of nutrient species for each of the six plant organ pools:

Leaf
Fine-root
Sapwood
Structural wood
Storage
Reproductive

The PARTEH code for hypothesis two currently only enables Nitrogen and Phosphorous. The code can be easily extended to handle other nurtient species, however this would increase the number of parameters used and complicate things for a broader user base. Without an imediate need for other species, they have been left out. This documentation will use the generic symbol $N$ for all nutrients of any species indexed by $s$ in organs indexed by $o$ .

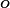The state variables, boundary conditions and parameters for hypothesis 2 are described in Table H2-1.

Table 1.5 Table H2-1¶
Symbol	Dimension	Description	Units
State Variables
$C_{(o)}$	organ	carbon mass	[kg]
$N_{(o,s)}$	organ x species	nutrient mass	[kg]
Input/Output Boundary Conditions
$R_{md}$	scalar	Maint. Resp. Deficit	[kg]
$d$	scalar	Reference Stem Diameter	[cm]
Input Boundary Conditions
$f_{trim}$	scalar	Canopy Trim Fraction	[0-1]
$C_{gain}$	scalar	Daily carbon gain	[kg]
$N_{gain(s)}$	species	Daily nutrient gain	[kg]
Output Boundary Conditions
$C_{exu}$	scalar	Daily carbon exudation	[kg]
$N_{exu(s)}$	species	Daily nutrient exudation	[kg]
$R_g$	scalar	Growth Respiration	[kg]
Parameters
$\alpha_{(o,s)}$	pft* x organ x species	ideal stoichiometric ratios	[kg/kg]
$\beta_{(o,s)}$	pft* x organ x species	minimum stoichiometric ratios	[kg/kg]
$p_{tm}$	pft*	tissue vs. resp. prioritization	[0-1]
$\omega_{(o)}$	pft* x organ	prioritization level	[1-6]
$r_{g(o)}$	pft* x organ	unit growth respiration rate	[kg/kg]

List of key states, boundary conditions and parameters in hypothesis 2, allometric multi-nutrient species with fixed target stoichiometry. In this notation, o and s are used to index the organ and species (nutrient) dimensions. :math:`*` Note that the parameters are specified explicitly for each pft, but the dimension will be implied in our notation as each plant is already uniquely asociated with a PFT.

1.5.2.2.2.1. Order of Operations¶

It is assumed that over the sub-daily time-steps, photosynthesis, respiration and nutrient uptake has been accumulated. These provide net carbon and nutrient gains at the end of the day to drive allocations. The first daily procedure is the removal of biomass from the plant due to turnover coming from leaf-fall, branchfall and turnover of fine-roots. The second daiy procedure seeks to replenish the plants existing pools with respect to a target mass that is defined by the stature (size) of the plant (this may be thought of of bringing the plant back to allometric targets). Next, if resources are still available the plant will grow in stature, where allocation seeks to grow the pools out concurrently with each other. If any nutrient resources remain, they will be allocated towards ideal stoichiometric proportions, which may or may not be greater than the proportionalities needed during stature growth. And finally, all excess materials are sent to storage pools (if not full) and then exuded through roots.

(sub-daily) Accumulate Carbon and Nutrients
(daily) Perform Allocations to Pools

VISUALIZATION

1.5.2.2.2.2. Accumulate Carbon and Nutrients¶

Photosynthesis and maintenance respiration are sensitive to light levels and tissue temperatures, which vary over sub-daily timescales. In CLM/ELM, this “fast” time-step is 30 minutes. It is assumed that the host-model (e.g. FATES) will handle the calculation of GPP and maintenance respiration, and integrate these quantities over the course of the day. There is some flexibility in how PARTEH handles allocations with these two constraints. Along with nutrient inputs, the host model must provide the boundary conditions of daily carbon gain 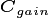$C_{gain}$ , and optionally, the maintenance respiration deficit $R_{md}$ .

There are two scenarios that this hypothesis accomodates:

The host model calculates the difference between daily integrated GPP and maintenance respiration and passes it as 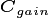$C_{gain}$ , which may be positive or negative. No maintenance respiration is tracked, because it is paid instantly, and thus $R_{md} = 0$ .
The host model passes GPP as 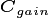$C_{gain}$ (always positive), and maintains a running account of maintenance respiration deficit, thereby adding the daily integrated maintenance respiration to $R_{md}$ . The PARTEH model will then attempt to pay for $R_{md}$ , and passing back the updated deficit to the host.

The third key boundary condition provided by the host, is the daily integrated flux of nutrients from soil to fine-roots, $N_{gain(s)}$ , for each nutrient species $s$ . Depending on the soil biogeochemistry model in use, PARTEH can provide information about the state of the plant, to help the soil biogeochemistry module determine the plant’s affinity in a competitive nutrient environment.

1.5.2.2.2.3. Remove Biomass From All Pools as Turnover¶

Different methodologies for calculating turnover exist, and are executed prior to allocations. Event based turnover is covered in Event Based Turnover Hypotheses, and maintenance turnover is covered in Maintenance Turnover Hypotheses.

1.5.2.2.2.4. Replenish Pools with Respect to Target Levels¶

The organs of each plant have target masses for carbon $\grave{C}_{(o)}$ and nutrients $\grave{N}_{(o,s)}$ . These targets are goverened by the stature of the plant, and can be thought of as the desireable pool sizes that the plant would like to have to be ready for further growth in stature. Turnover, as described in the previous section, draws down the masses away from the target values associated with their current stature. Sometimes this is considered being “off allometry”. In this hypothesis, the base assumption is that the targets are dictated by allometry, but other methods of determining these targets are possible as well. 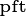Allometric targets are typically a function of plant diameter $\text{dbh}$ , plant functional type $\text{pft}$ , and an indicator of how much trimming of unproductive lower boughs a plant has executed $\text{trimming}$ .

(1.21)¶ $\grave{C}_{(o)} &= \text{func}(\text{dbh},\text{pft},\text{trimming})$

For nutrient species, the targets are based on a parameter that describes the minimum stoichiometric ratios with carbon $\beta_{(o,s)}$ that are required for the plant to grow in stature.

(1.22)¶ $\grave{N}_{(o,s)} &= \quad \grave{C}_{(o)} \cdot \beta_{(o,s)}$

In this step, the plant must allocate resources to bring its pools up to the targets before growing out the plant’s stature again. This process relies on calculating the targets, and then the carbon $\check{C}_{(o)}$ and nutrient $\check{N}_{(o,s)}$ demands to reach those targets.

Given these targets, the demands for each carbon $\check{C}_{(o)}$ and nutrient $\check{N}_{(o,s)}$ pool are calculated. In the case of carbon, a growth tax is applied to allocation, which contributes to the demand. Here, that tax is governed by a unit growth parameter $r_{g(o)}$ , however more complicated growth tax functions could be used as well. Likewise, a pool may already be at or above its current target. Only positive demands are used, so a floor of 0 is imposed on the demand.

(1.23)¶ $\check{C}_{(o)} &= \quad \text{max}(0,(\grave{C}_{(o)} - C_{(o)}) \cdot (1+r_{g(o)}))$

(1.24)¶ $\check{N}_{(o,s)} &= \quad \text{max}(0,\grave{N}_{(o,s)} - N_{(o,s)} )$

Each plant organ is then associated with any priority level, 0 through 6. Organs associated with priority 1 will get first access to carbon and nutrients and organs associated with priority order will get the remainder. The priority order levels are ascended sequentially, we indicate the valid set of organ indices in the current priority order level $pr$ as set $\mathbb{O}_{pr}$ . Note that priority level 0 is a special bypass level. This is used for reproductive allocation, which currently is only generated during the stature growth step. Note, it is not required that ANY organs are classified as priority 1.

The first priority level ( $pr=1,\mathbb{O}_{1}$ ) has two approaches based on the boundary conditions provided.

It is assumed that maintenance respiration costs have not been paid yet by the host model, and thus the maintenance respiration deficit $R_{md}$ exists and is non-zero, and that daily carbon gains are greater than or equal to zero. This is detailed in Priority 1 Carbon Fluxes with explicit Maintenance Respiration Deficit.
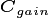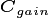It is assumed that boundary condition for $C_{gain}$ has already decucted maintenance respiration costs. Here, $R_{md}$ is always zero, and if the plant is not metabolically dormant, $C_{gain}$ may be positive or negative. This is detailed in :ref:”p1_implicit_rmd_section’.

1.5.2.2.2.4.1. Priority 1 Carbon Fluxes with explicit Maintenance Respiration Deficit¶

First, we assess how much total demand is coming from the priority 1 carbon pools.

(1.25)¶ $\check{C}_1 &= \sum_{o=\mathbb{O}_{1}} \check{C}_{(o)}$

The total carbon that can be translocated from storage is $\vec{C}_{st-tran}$ . Any number of models could be used to determine how resistant the storage is to pay off high-priority tissues and maintenance respiration costs. Below is an example of a simple function where the transferable carbon decreases as the square of the pool’s proportion with its target. Where storage is denoted organ index $o=st$ :

(1.26)¶ $C_{st-tran} &= C_{(st)} \cdot \text{min}(1,C_{(st)} / \grave{C}_{(st)} )$

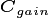The total carbon that is transferred $\vec{C}_{tot}$ is the minimum between the demanded and what can be transferred from both storage and carbon gains $C_{gain}$ . The fraction of how much is transferred versus demanded, $f_{tot}$ , is also useful.

(1.27)¶ $\vec{C}_{tot} &= \quad \text{min}( \check{C}_1 + R_{md} , C_{st-tran} + C_{gain} ) f_{tot} &= \quad \vec{C}_{tot} / (\check{C}_1 + R_{md})$

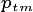Preference can be specified to allocate available carbon to either maintenance respiration, or the priority 1 pools. To do so, we define a redistribution flux $\vec{C}_{RD}$ that scales the transfer between the two options. The parameter $p_{tm}$ , which varies betwen 0 and 1, sets the relative priority of each. When the parameter is greater than 0.5, $\vec{C}_{RD}$ re-directs flux from relieving maintenance respiration deficit ( $\vec{C}_{md}$ ) towards priority 1 tissues ( $\vec{C}_1$ ). Alternatively, when the parameter is less than 0.5, $\vec{C}_{RD}$ is redictect from replacing priority 1 tissues into maintenance respiration deficit.

(1.28)¶ $\text{for }p_{tm}>0.5 \vec{C}_{RD} &= \quad \text{min}( (p_{tm}-0.5)/0.5 \cdot f_{tot} \cdot R_m, (1-f_{tot}) \cdot \check{C}_1 ) \vec{C}_1 &= \quad f_{tot} \cdot \check{C}_1 + \vec{C}_{RD} \vec{R}_{md} &= \quad f_{tot} \cdot R_{md} - \vec{C}_{RD} \text{for }p_{tm}<0.5 \vec{C}_{RD} &= \quad \text{min}( (0.5-p_{tm})/0.5 \cdot f_{tot} \cdot \check{C}_1, (1-f_{tot}) \cdot R_{md} ) \vec{C}_1 &= \quad f_{tot} \cdot \check{C}_1 - C_{RD} \vec{R}_{md} &= \quad f_{tot} \cdot R_{md} + \vec{C}_{RD}$

The total flux of carbon into each priority 1 pool is then governed, linearly, by the fraction of which their demand constitutes the whole demand. For any carbon pool in organ found in priority set $\mathbb{O}_1$ .

(1.29)¶ $\vec{C}_{(\mathbb{O}_1)} &= \vec{C}_1 \cdot \check{C}_{(\mathbb{O}_1)} / \check{C}_1$

With the fluxes known, increment the priority 1 carbon pools, increment their growth respiration. For each organ in set $\mathbb{O}_1$ :

(1.30)¶ $C_{(\mathbb{O}_1)} &= \quad C_{(\mathbb{O}_1)} + \vec{C}_{(\mathbb{O}_1)} / (1+r_{g(\mathbb{O}_1)}) R_{g(\mathbb{O}_1)} &= \quad R_{g(\mathbb{O}_1)} + \vec{C}_{(\mathbb{O}_1)} \cdot r_{g(\mathbb{O}_1)} / (1+r_{g(\mathbb{O}_1)})$

Decrement maintenance respiration deficit, daily carbon gain, and potentially, storage carbon (where $o=st$ ).

(1.31)¶ $R_{md} &= \quad R_{md} - \vec{R}_{md} \vec{C}_{gain} &= \quad \text{min}(C_{gain}, \vec{C}_{tot}) C_{gain} &= \quad C_{gain} - \vec{C}_{gain} C_{(st)} &= \quad C_{(st)} - \text{max}(0, \vec{C}_{tot} - \vec{C}_{gain})$

1.5.2.2.2.4.2. Priority 1 Carbon Fluxes with Implicit Maintenance Respiration¶

Recall that as an alternative to Priority 1 Carbon Fluxes with explicit Maintenance Respiration Deficit, carbon gains may subsume maintenance respiration. With this assumption, the equations in the previous section are valid in all cases, except for when $C_{gain} < 0$ . For this condition, it is assumed that storage carbon will pay off the negative carbon gain and bring it back to zero. Caution must be made, in so much that calculations of maintenance respiration are conducted so that the plant does create impossible conditions where storage carbon becomes zero. PARTEH will fail gracefully in this condition. The remainder of this section specifically details the condition where $C_{gain}<0$ .

The flux from storage brings negative daily carbon gain up to zero.

(1.32)¶ $\vec{C}_{gain} &= \quad - C_{gain} C_{(st)} &= \quad C_{(st)} - \vec{C}_{gain} C_{gain} &= 0$

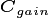Any extra flux that can transferred out of storage and into priority 1 tissues, would then be calculated by using the same function that determines the maximum transferrable carbon, as in (1.26). However, in this case $C_{st-trans}$ is calculated after the carbon to replace the negative $C_{gain}$ is removed in (1.32). The demand for carbon to priority 1 tissues follows the same methods as Priority 1 Carbon Fluxes with explicit Maintenance Respiration Deficit.

(1.33)¶ $\text{if} \quad C_{gain} < 0 \vec{C}_1 &= \quad \text{min}(C_{st-trans},\check{C}_1)$

Transfer from storage into priority 1 tissues also follows the same logic as Priority 1 Carbon Fluxes with explicit Maintenance Respiration Deficit, specifically (1.29). And finally, decrement storage again, as per total flux into priority 1 organs $\vec{C}_1$ .

(1.34)¶ $C_{(st)} &= \quad C_{(st)} + \vec{C}_{1}$

1.5.2.2.2.4.3. Priority 1 Nutrient Fluxes¶

With the priority 1 carbon pools updated, the fluxes of nutrients into those pools can proceed. The targets $\grave{N}_{(o,s)}$ , and subsequently the deficit from the target $\check{N}_{(o,s)}$ , is set by the organ of interest’s current (and newly updated) carbon mass. For all nutrient species $s$ , and all organs 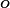$o$ in set $\mathbb{O}_1$ , the targets and demands are updated via (1.22) and (1.24).

The total demand for each nutrient species $s$ across priority 1 tissues is thus:

(1.35)¶ $\check{N}_{1(s)} = & \quad \sum_{o=\mathbb{O}_{1}} \check{N}_{(o,s)}$

And therefore the fluxes for each species $s$ and each organ in priority set $\mathbb{O}_1$ are transferred into their respective pools.

(1.36)¶ $\vec{N}_{(\mathbb{O}_1,s)} = & \quad \text{min}(N_{gain(s)},\check{N}_{1(s)}) \cdot ( \check{N}_{(\mathbb{O}_1,s)} / \check{N}_{1(s)} ) N_{(\mathbb{O}_1,s)} = & \quad N_{(\mathbb{O}_1,s)} + \vec{N}_{(\mathbb{O}_1,s)}$

The daily nutrient gains for each species are correspondingly decremented.

(1.37)¶ $N_{gain(s)} = & \quad N_{gain(s)} - \text{min}(N_{gain(s)},\check{N}_{1(s)})$

1.5.2.2.2.4.4. Carbon and Nutrient Fluxes after Priority Level 1¶

At this point, all priority 1 fluxes have been allocated. The next priority level fluxes are enacted sequentially, and the procedure is much the same as priority 1, without the complications of shunting carbon to maintenance respiration or paying back negative carbon gains, or transfering from storage to pay for priority 1 demands.

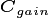For each priority level $pr$ , a new set of organs is sub-set into group $\mathbb{O}_{pr}$ , thereby calculating fluxes of carbon and nutrients and decrementing $C_{gain}$ and $N_{gain(s)}$ correspondingly. The algorithm follows generally:

Sum the carbon demands of the set, via (1.25)
Calculate carbon fluxes based on relative demand, similar to (1.29)
Increment carbon pools, growth respiration and decrement carbon gain, via (1.30) and (1.31) (ignoring parts where storage is translocated)
Re-assess nutrient demands, via (1.24)
Sum the nutrient demands of the set, similar too (1.35)
Calculate nutrient fluxes and perform transfers, similar to (1.36) and (1.37)

1.5.2.2.2.5. Grow Stature Concurrently¶

If there is at some of each daily carbon gain, and daily nutrient gain for all species remaining, the plant will grow out its stature. This method assumes that the organs will grow out concurrently.

As a default, the carbon in these organs will be allocated as dictated by the derivatives of the allometric functions. Other hypotheses, such as those that seek to optimize root tissues to increase nutrient acquisition will break from this.

Of important note, is that for either reasons governed outside of the PARTEH framework, or because of numerical integration errors, some organs may have slightly more carbon than their allometric target. In doing so, we remove these organs from the set to be grown out. Structural carbon is an exception, and is always “on-allometry”, since it is directly tied to stature and dbh. This is actually forced by adjusting the plant’s diameter to match the structural carbon in cases where structural carbon was higher than its allometric target.

Broadly, the first objective in this section, is to determine which species, be it carbon or nutrient, will limit growth. To do this, we calculate an approximation of how much equivalent growth in carbon each of them could provide, by extrapolating the derivatives at the current plant’s stature. The derivatives for target carbon per change in diameter, $\frac{dC_{(o)}}{dd}$ , are provided by allometric functions. 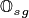In the following set of organs, we exlude reproduction (which does not have a derivative wrt size), creating subset of organs $\mathbb{O}_{sg}$ .

(1.38)¶ $\frac{dC_{sg}}{dd} =& \quad \sum_{o=\mathbb{O}_{sg}} \frac{d\grave{C}_{(o)}}{dd}$

With this sum, we can determine the relative fraction of carbon that is sent to each organ in set 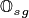$\mathbb{O}_{sg}$ , that is directed to stature growth, denoted: $f_{sg(\mathbb{O}_{sg})}$ . The fraction of flux that is directed towards reproductive organs, $f_{sg(o=repro)}$ is special, and is calculated from an external module.

For the other organs, in set 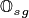$\mathbb{O}_{sg}$ :

(1.39)¶ $f_{sg(\mathbb{O}_{sg})} &= \frac{d\grave{C}_{(\mathbb{O}_{sg})}}{dd} / \frac{dC_{sg}}{dd} \cdot (1 - f_{sg(repro)})$

The approximated amount of carbon would be transferred into plant tissues $\vec{C}^*_{sg}$ , is calculated via assembling these relative fractions, and divesting the total available carbon gain of the growth respiration rates for each pool. Note the asterisk in the symbology is meant to reflect an approximate value.

(1.40)¶ $\vec{C}^*_{sg} \quad &= \quad C_{gain} \cdot \left( \frac{ f_{sg(repro)} }{ 1 + r_{g(repro)}} + \sum_{o=\mathbb{O}_{sg}} \frac{ f_{sg(o)} }{ 1 + r_g(o) } \right)$

The approximated amount of nutrient of each species $s$ that would be transferred into plant tissues $\vec{N}^*_{sg(s)}$ , is calculated much in the same way, however there is no growth respiration tax. Also, it is possible that a nutrient pool may have a mass that is already greater than the mass equivalent to the target associated with the minimum stoichiometry. Such cases must be accounted for, because they will reduce the likelihood of nutrient needs in that organ limiting growth.

(1.41)¶ $\vec{N}^*_{sg(s)} \quad &= \quad N_{gain(s)} \cdot \left( f_{sg(repro)} / \beta_{(repro,s)} + \sum_{o=\mathbb{O}_{sg}} f_{sg(o)} / \beta_{(o,s)} \right) \\ &+ \quad \text{max}(0,N_{(repro,s)} - \grave{N}_{(repro,s)}) / \beta_{(repro,s)} \\ &+ \quad \sum_{o=\mathbb{O}_{sg}} \text{max}(0,N_{(o,s)} - \grave{N}_{(o,s)}) / \beta_{(o,s)}$

The actual carbon that is then set aside for stature growth $\vec{C}_{sg}$ , based on the minimum of approximations $\vec{C}^*_{sg}$ and $\vec{N}^*_{sg(s)}$ .

(1.42)¶ $\vec{C}_{sg} &= \quad C_{gain} \cdot \text{min}( \vec{C}^*_{sg}, \vec{N}^*_{sg(s)} ) / \vec{C}^*_{sg}$

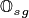Carbon fluxes into each of the plant’s organs are conducted via numerical integration, which is a coupled set of ordinary differential equations, integrated over $\vec{C}_{sg}$ . For each organ in set $\mathbb{O}_{sg}$ .

Where the rate of change of carbon for a given organ is its proportionality relative to the whole:

(1.43)¶ $\frac{d C_{(\mathbb{O}_{sg})}}{d C_{sg}} &= \quad \overbrace{\frac{dC_{(\mathbb{O}_{sg})}}{dd} \cdot \frac{dd}{d C_{sg}}}^{ \text{Continuous allometry equations} }$

(1.44)¶ $\vec{C}_{sg(\mathbb{O}_{sg})} &= \quad \int_{dC_{sg}=0}^{\vec{C}_{sg}} \frac{d C_{(\mathbb{O}_{sg})}}{d C_{sg}} dC_{sg}$

The fluxes are then transferred to increment the carbon pools, increment the growth respiration and decrement the carbon gain.

1.5.2.2.2. Allocation Hypothesis 2: Allometrically Guided, Carbon and Nutrients with Prioritization and Flexible Target Stoichiometry¶

1.5.2.2.2.1. Order of Operations¶

1.5.2.2.2.2. Accumulate Carbon and Nutrients¶

1.5.2.2.2.3. Remove Biomass From All Pools as Turnover¶

1.5.2.2.2.4. Replenish Pools with Respect to Target Levels¶

1.5.2.2.2.4.1. Priority 1 Carbon Fluxes with explicit Maintenance Respiration Deficit¶

1.5.2.2.2.4.2. Priority 1 Carbon Fluxes with Implicit Maintenance Respiration¶

1.5.2.2.2.4.3. Priority 1 Nutrient Fluxes¶

1.5.2.2.2.4.4. Carbon and Nutrient Fluxes after Priority Level 1¶

1.5.2.2.2.5. Grow Stature Concurrently¶

1.5.2.2.2.6. Allocate Nutrients Towards Ideal Stoichiometric Ratios¶

1.5.2.2.2.7. Send Excess Quantities to Storage or Exude to Soil¶

Table of Contents

Previous topic

Next topic

This Page